Задача 75918 ...

65d4a8a258f8d021aead7dc2

2/20/2024 1:27:48 PM

З вершини прямого кута C трикутника ABC проведено перпендикуляр
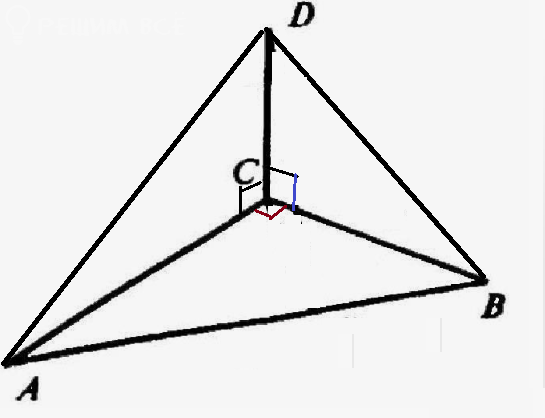
CD до площини трикутника. DB і DA - похилі.

Відомо, що:

CD = 1см;
DB= 3см;
DA= √3 см.

Знайти:
1. довжину невідомої похилої;
2. довжину невідомої проекції;
3. довжину відрізка АВ;
4. довжину медіани CM;
5. довжину відрізка DM;
6. відстань від точки В до площини DCM.

5f3ea7e3faf909182968ddd9

2/21/2024 5:39:02 AM

★

CD ⊥ плоскости АВС ⇒ СD ⊥ BC и СD ⊥ AC


Δ CDB - прямоугольный

по теореме Пифагора

CB^2=DB^2-DC^2=3^2-1^2=8



Δ CDA - прямоугольный

по теореме Пифагора

CA^2=DA^2-DC^2=(sqrt(3))^2-1^2=2


Δ ABC - прямоугольный

по теореме Пифагора

AB^2=BC^2+AC^2=8+2=10

AB=sqrt(10)



Медиана СМ прямоугольного треугольника

CM=AB/2=sqrt(10)/2


DM^2=DC^2+DM^2=1^2+(sqrt(10)/2)^2=1+(10/4)=14/4

DM=sqrt(14)/2


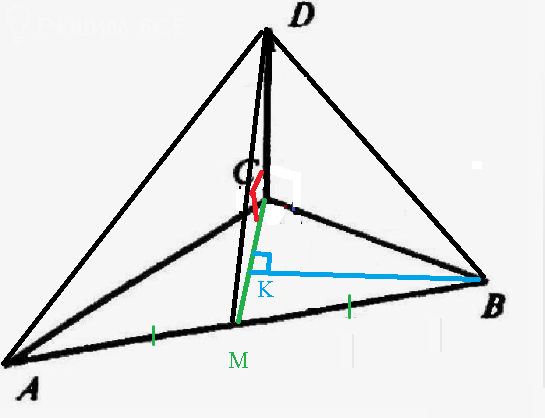
BK ⊥ CM

DC ⊥ плоскости АВС ⇒ DC ⊥ BK


BK ⊥ двум пересекающимся прямым плоскости DCK ⇒ [b]BK перпендикулярна плоскости DCK[/b]


BK -[b] расстояние[/b] от точки В до плоскости DCK


Δ CMB равнобедренный
СM=BM=sqrt(10)/2
BC=sqrt(8)

Проведем MP ⊥ CB
Получим прямоугольный треугольник MPB

По теореме Пифагора

MP^2=(sqrt(10)/2)^2-(sqrt(8)/2)^2=(10/4)-(8/4)=2/4

MP=sqrt(2)/2


S_( Δ PCB)=(1/2)BC*MP

S_( Δ PCB)=(1/2)CM*BK


(1/2)BC*MP=(1/2)CM*BK


⇒ BK=sqrt(8)*sqrt(2)/sqrt(10)=16/sqrt(10)=16sqrt(10)/10=[b]8sqrt(10)/5[/b]