Задача 57183 Помогите пожалуйста!!!В правильной...

6006d68784fa39088070e4e6

19.01.2021 21:12:44

Помогите пожалуйста!!!В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 30 ° Найдите высоту пирамиды, если радиус описанной вокруг ее сферы равен 4

5f3ea7e3faf909182968ddd9

19.01.2021 22:00:38

★

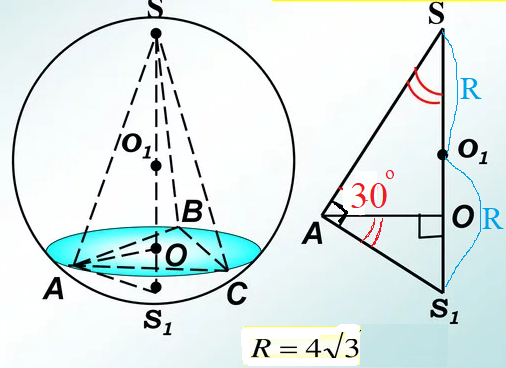
SO_(1)=O_(1)S_(1)=R=4 ⇒

SS_(1)=[b]8[/b]

O-центр окружности описанной около Δ АВС

Δ ABC - равносторонний.

Пусть [b]АВ=BC=AC=a[/b]

AO=r=[blue][b]a*sqrt(3)/3[/b][/blue] - радиус окружности описанной около Δ АВС


Из прямоугольного треугольника АОS с углом в 30 ° :

SO=AO*tg30 ° =a*(sqrt(3)/3)*sqrt(3)/3=[b]a/3[/b]


Тогда
S_(1)O=SS_(1)-SO=[red][b]8-(a/3)[/b][/red]

По свойству высоты, проведенной из вершины прямого угла:

AO^2=SO*OS_(1)

[blue][b](a*sqrt(3)/3)^2[/b][/blue]=[b](a/3)[/b]*[red][b](8-(a/3))[/b][/red]


a^2/3=a*8/3-(a^2/9)

4a/9=8/3

a=6


SO=a/3=6/3=[b]2[/b]