Задача 58152 ...

602ea5793cfdeb46290ca5ae

27.02.2021 19:17:14

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ даны длины рёбер:
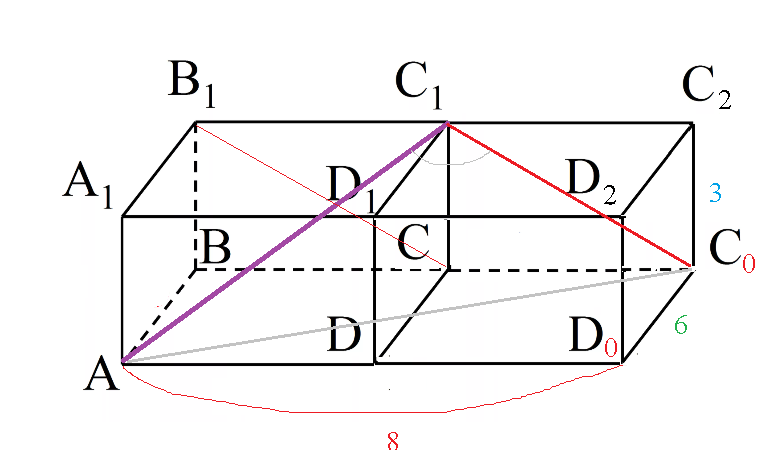
AB=6, BC=4, AA₁=3. Найди угол между прямыми AC₁ и B₁C.

5f3ea7e3faf909182968ddd9

27.02.2021 23:30:03

★

С_(1)С_(0) || B_(1)C

Угол между AC_(1) и B_(1)C равен углу между AC_(1) и С_(1)С_(0)

Находим его по теореме косинусов из Δ АС_(1)С_(0)

Для этого находим стороны треугольника:

AC_(1)=sqrt(6^2+4^2+3^2)=sqrt(61)

B_(1)C=sqrt(3^2+4^2)=5

AC_(0)=sqrt(6^2+*^2)=10

Тогда

AC^2_(0)=AC^2_(1)+C_(1)C^2_(0)-2*AC_(1)*C_(1)C_(0)* cos ∠ AC_(1)C_(0) ⇒

cos ∠ AC_(1)C_(0)=(AC^2_(1)+C_(1)C^2_(0)-AC^2_(0))/(2*AC_(1)*C_(1)C_(0))


cos∠ AC_(1)C_(0)=(61+25-100)/(2sqrt(61)*5)=-7/(5*sqrt(61))