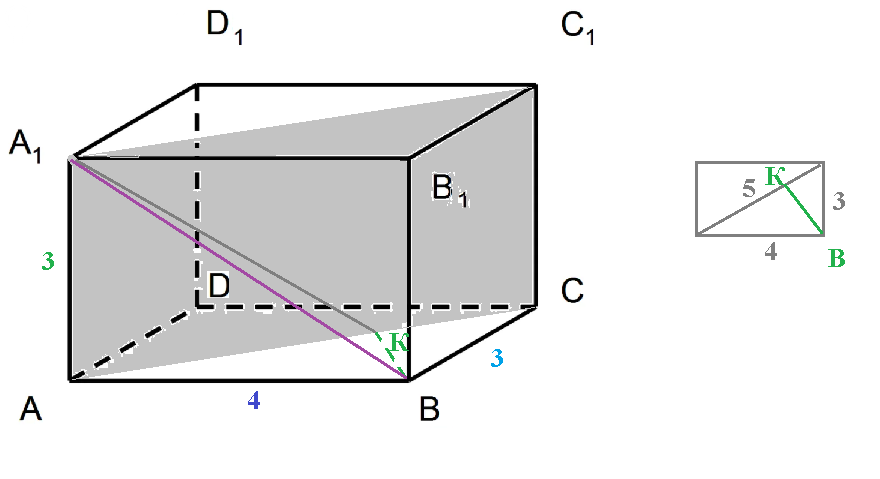
Задача 64504 В прямоугольном параллелепипеде...

627bb760ee12fc22d71dddc8

11 мая 2022 г. в 16:18

В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью АА1Си прямой А1В, если АА1=3, АВ=4, ВС=3

exponenta

11 мая 2022 г. в 18:48

★

Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость.

Найдем проекцию прямой А₁B на плоскость АА1С₁С

Проводим BK ⊥ AC

АА₁ ⊥ АBСD ⇒ АА₁ ⊥ BK


BK ⊥ AC
BK ⊥ АА₁

BK перпендикулярна двум пересекающимся прямым плоскости АBСD ⇒BK перпендикулярна плоскости АBСD

А₁К– проекция А₁B на плоскость АА1С₁С

∠ ВА₁К можно найти из прямоугольного треугольника ВА₁К

АС=5

(АС²=AB²+BC²=4²+3²=16+9=25)


BK– высота прямоугольного треугольника АВС.

ВК=AB·BC/AC=4·3/5=12/5=2,4

A₁B=5

(А₁B²=AB²+AA₁²=4²+3²=16+9=25)

sin∠ ВА₁К=BK/A₁B=2,4/5=24/50=48/100


∠ ВА₁К=arcsin0,48