Задача 64878 ›т всех вершин < ©0 стороной 12 сми ЯНИИ...

6293dcdd64b30d7e93d2d542

29.05.2022 23:53:33

›т всех вершин < ©0 стороной 12 сми ЯНИИ # см от ПЛоСКостИ ' Расстояние от угольника. на расстоянии 6 см от 1е СА и СВ образуют с лы 30° и 45° соответственно, - "ние между точками А и В, если оекциями наклонных равен 30°. оао а [ - ч J‘.

5f3ea7e3faf909182968ddd9

30.05.2022 12:41:52

★

1. Точка D- равноудалена от всех вершин треугольника, Значит DA=DB=DC

Равные наклонные имеют равные проекции, значит проекция точки D на плоскость треугольника - точка О, которая является центром описанной окружности.

R=AO=BO=CO


DO=4 cм

АВ=ВС=АС=12 см

R=asqrt(3)/3


R=12sqrt(3)/3=[b]4sqrt(3)[/b]


DA=DB=DC

DA^2=DO^2+AO^2=4+([b]4sqrt(3)[/b])^2=4+48=52

DA=[b]2sqrt(13)[/b]

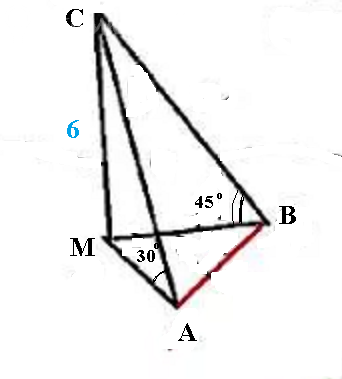
2. Пусть М- проекция точки С на пл. α

СМ=6

∠ САМ=30 °

∠ СВМ=45 °


Δ СВМ- прямоугольный равнобедренный ⇒ МВ=СМ=6

Δ САМ- прямоугольный с углом в 30 ° ⇒ катет против угла в 30 ° равен половине гипотенузы

АМ=х

СА=2х

По теореме Пифагора

CA^2=CM^2+МА^2

(2х)^2=6^2+x^2

3x^2=36

x^2=12

x=2sqrt(3) ⇒ АМ=2sqrt(3)


В треугольнике АВМ:

АМ=2sqrt(3)

ВМ=6

∠ АМВ=30 °

По теореме косинусов

AB^2=AM^2+BM^2-2*AM*BM*cos ∠ AMB

AB^2=(2sqrt(3))^2+6^2-2*2sqrt(3)*6*cos 30 °

AB^2=12+36-18=30

AB=sqrt(30)