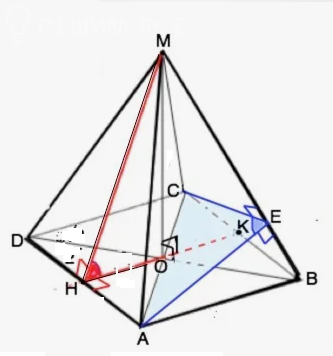
Задача 77596 Угол между боковой гранью правильной...

664e51e6d915332e35316351

5/22/2024 8:15:56 PM

Угол между боковой гранью правильной пирамиды S ABCD и плоскостью основания равен 30°. Найди косинус угла между боковыми гранями пирамиды.

5f3ea7e3faf909182968ddd9

5/23/2024 5:59:37 AM

★

MABCD- правильная пирамида
АВСD- квадрат

∠ МНО=30 °

Пусть сторона основания равна x

АВ=ВС=СD=AD=x
OH=(1/2)AB=x/2

Из прямоугольного треугольника МНО
МО=НО*tg30=(x/2)*sqrt(3)/3=xsqrt(3)/6
MH=2MO= [b]x*sqrt(3)/3[/b] ( катет против угла в 30 ° равен половине гипотенузы)



h=[b]x*sqrt(3)/3[/b] - [i]апофема боковой грани[/i]



AC=BD=x*sqrt(2) - диагонали квадрата ABCD

Из прямоугольного треугольника МОА

MA^2=MO^2+AO^2=(xsqrt(3)/6)^2+(x*sqrt(2)/2)^2=(3x^2/36)+(2x^2/4)=7x^2/12

MA=xsqrt(7)/sqrt(12)


Из равнобедренного треугольника MAB

AE* MB=AB*h

MB=MA=xsqrt(7)/sqrt(12)

AE=2x/sqrt(7)


Из равнобедренного треугольника AEC

по теореме косинусов

cos ∠ AEC=(AE^2+EC^2-AC^2)/(2*AE*EC)=-3/4=[b]-0,75[/b]