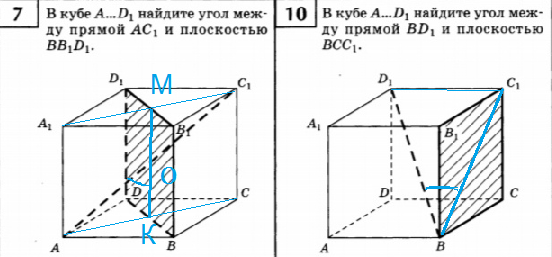
Задача 34765 7. В кубе А...D1, найдите угол между...
Условие
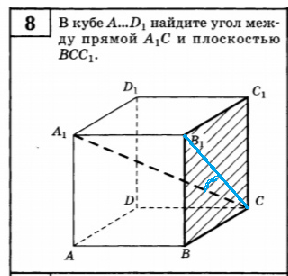
8. В кубе A...D1, найдите угол между прямой А1С и плоскостью BCC1.
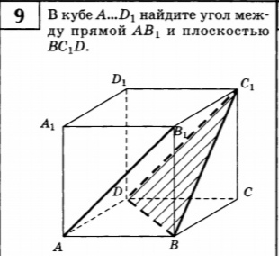
9. В кубе А...D1, найдите угол между прямой АВ1, и плоскостью BC1D
10. В кубе А...D1, найдите угол между прямой BD1 и плоскостью ВСС1.
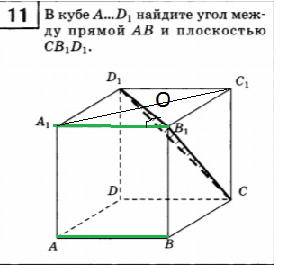
11. В кубе А...D1, найдите угол между прямой АВ и плоскостью СВ1D1.
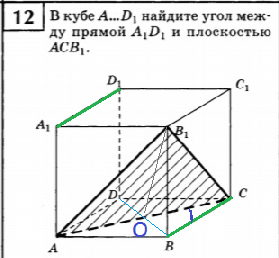
12. В кубе А...D1, найдите угол между прямой А1D1 и плоскостью АСВ1.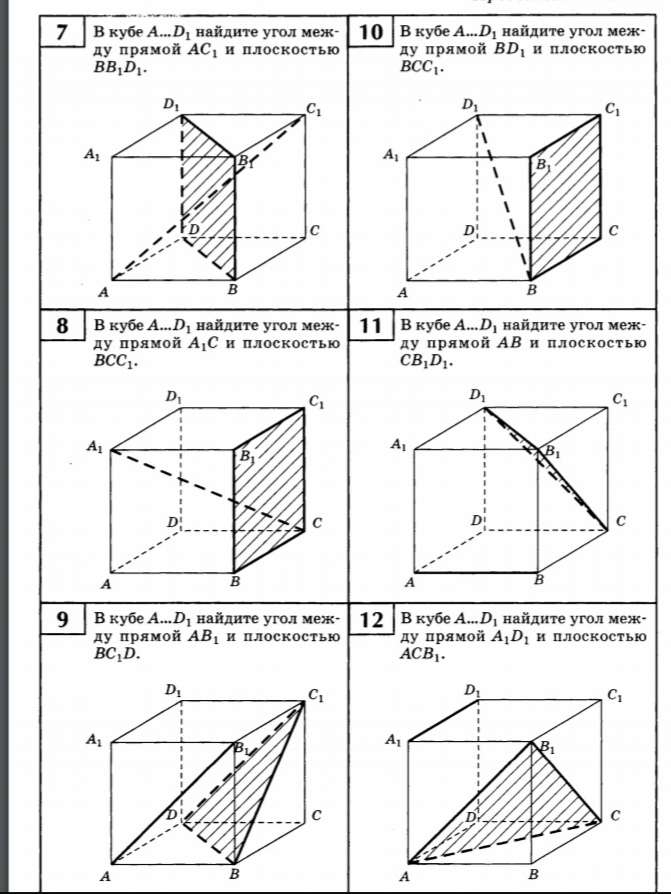
Решение
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость.
Проводим A_(1)C_(1) ⊥ B_(1)D_(1)
и АС ⊥ BD
Проекцией АС_(1) является MK
Угол АОК - искомый, находим из треугольника AOK
[b]tg ∠ AOK[/b]=AK/OK=sqrt(2)/2/1/2= [b]sqrt(2)[/b]
АК=AC/2=sqrt(2)/2
ОК=(1/2)МК=1/2
О т в е т. ∠ AOK= arctg(sqrt(2))
10.
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость.
Проекцией BD_(1) является BС_(1).
Угол C_(1)BD_(1) - искомый, находим из треугольника C_(1)BD_(1)
tg ∠ C_(1)BD_(1)=C_(1)D_(1)/BC_(1)=1/sqrt(2)=sqrt(2)/2
∠ C_(1)BD_(1)=arctg (sqrt(2)/2)
О т в е т. ∠ C_(1)BD_(1)=arctg (sqrt(2)/2)
8.
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость.
Проекцией A_(1)C является B_(1)C.
Угол A_(1)BC_(1) - искомый, находим из треугольника A_(1)BC_(1)
tg ∠ A_(1)BC_(1)=A_(1)B_(1)/B_(1)C=1/sqrt(2)=sqrt(2)/2
∠∠ A_(1)BC_(1)=arctg (sqrt(2)/2)
О т в е т. ∠ A_(1)BC_(1)=arctg (sqrt(2)/2)
12.
BD ⊥ AC
AC⊥ BO
B_(1)O - медиана равнобедренного треугольника АВ_(1)С
Значит, B_(1)O⊥ AC
АС ⊥ пл. В_(1)ОВ, так как перпендикулярна двум пересекающимся прямым этой плоскости BO и B_(1)O.
пл. АВ_(1)С ⊥ пл. В_(1)ОВ
⇒ ОС- проекция ВС,
угол между ОС и ВС - это угол АСВ он равен 45 градусов
ВС || A_(1)D_(1)
Значит угол между A_(1)D_(1) и пл. АВ_(1)С равен 45 градусов
11.
Как в 12.
∠ А_(1)В_(1)О= 45 градусов.
9. AB_(1)|| DС_(1)
AB_(1) || пл. DС_(1)B
Значит угол между ними 0 градусов.