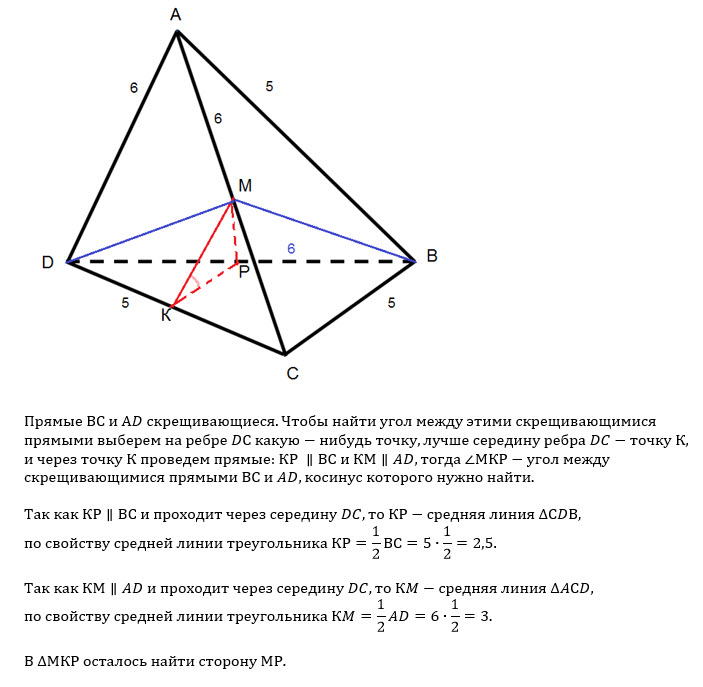
Задача 52955 Дан тетраэдр ABCD. Известно что...
Условие
Решение
со сторонами [b]5;5;6 [/b] и [b] 6;6;5[/b]
Проводим медианы МК и КР в треугольниках BDC и ADC.
МК || BC; [b]MК[/b]=2,5
KP || AD; [b] KP[/b]=3
[b] ∠ MKP[/b] - угол между скрещивающимися ребрами ВС и AD
найдем из треугольника МКР
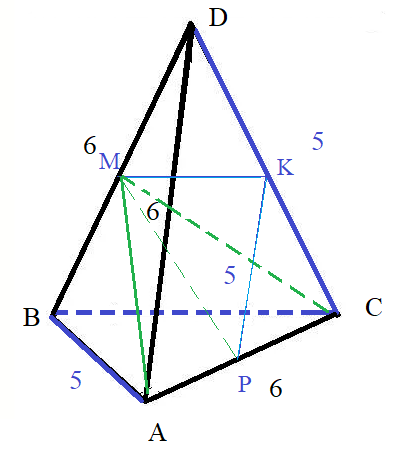
Для этого найдем третью сторону этого треугольника [b]МР.[/b]М
МР найдем из треугольника АМС.
Но сначала найдем медианы СМ и АМ в треугольниках СВD и АВD
CМ - медиана и высота равнобедренного треугольника АВD с основанием 6 и боковыми сторонами 5.
[b]СМ=4[/b]
Для нахождения АМ применяем метод [i]достраивания до параллелограмма
[/i] ( или метод удваивания медианы)
Тогда по свойству сторон и диагоналей параллелограмма:
[b]d^2_(1)+d^2_(2)=2(a^2+b^2)[/b]
[b](2AM)^2+BD^2=2(AB^2+AD^2)[/b] ⇒ (2AM)^2+6^2=2(5^2+6^2)
АМ=[m]\frac{\sqrt{86}}{2}[/m]
Для нахождения MP применяем метод [i]достраивания до параллелограмма [/i] ( или метод удваивания медианы)
[b](2MP)^2+AC^2=2(AM^2+CМ^2)[/b] ⇒ (2MP)^2+6^2=2(([m]\frac{\sqrt{86}}{2}[/m])^2+4^2)
4MP^2=39
[b]MP[/b]=[m]\frac{\sqrt{39}}{2}[/m]
Из Δ МКР по теореме косинусов:
МР^2=MK^2+KP^2-2*MK*KP*cos ∠MKP
[m]\frac{39}{4}=(\frac{5}{2})^2+3^2-2\cdot \frac{5}{2}\cdot 3 \cdot cos \angle MKP[/m]
[b]cos ∠MKP[/b]= [m]\frac{11}{30}[/m]
О т в е т. [m]\frac{11}{30}[/m]
Все решения