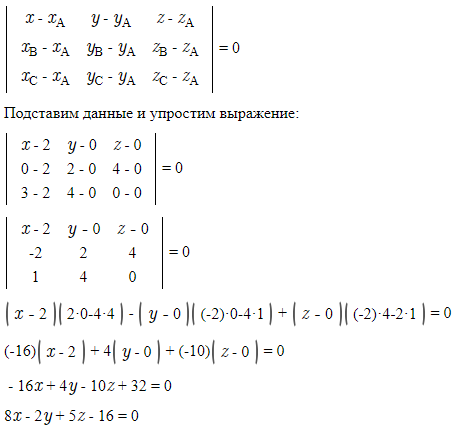Задача 55358 Решите 5, пожалуйста, методом координат...
Условие

математика 10-11 класс
503
Решение
★
a=4
5)
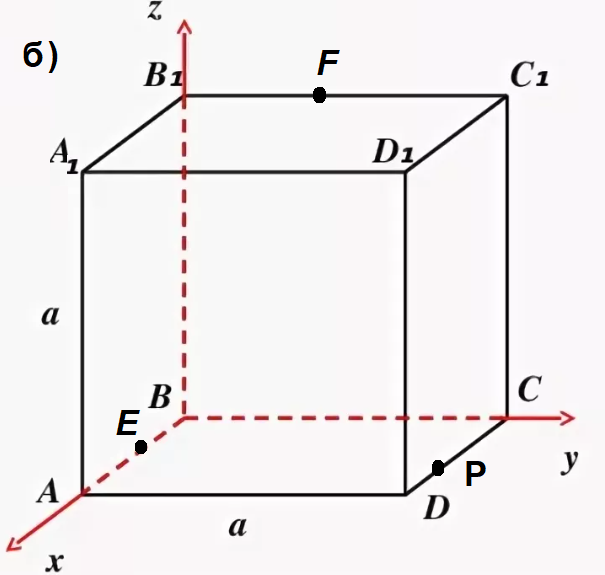
E (2;0;0); F(0;2;4);P(3;4;0)
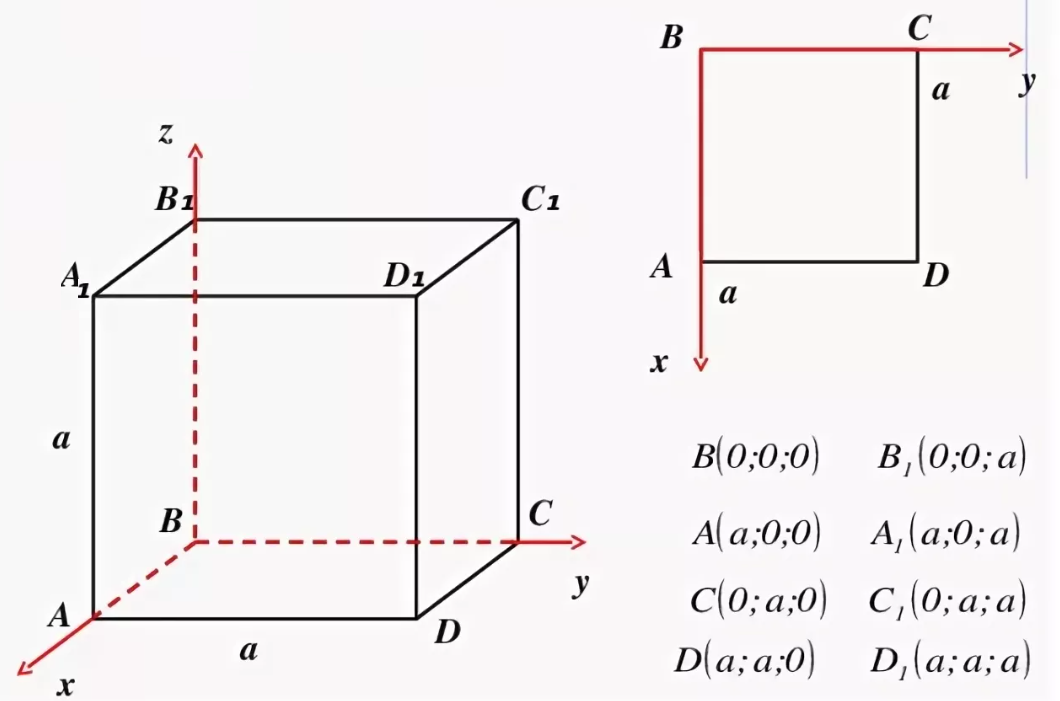
Составляем уравнение плоскости EFP как плоскости, проходящей через три точки ( см. скрин)
Угол между плоскостью EFP: [m]8x-2y+5z-16=0[/m] и плоскостью АВСD: [m] z=0[/m]
равен углу между их нормальными векторами:
[m]\vec{n_{1}}=(8;-2;5)[/m] и [m]\vec{n_{2}}=(0;0;1)[/m]
[m]cos ∠ (EFP,ABCD)=cos ∠ (\vec{n_{1}}, \vec{n_{2}})=\frac{\vec{n_{1}}\cdot \vec{n_{2}}}{|\vec{n_{1}}|\cdot | \vec{n_{2}}|}=\frac{5}{\sqrt{8^2+(-2)^2+5^2}\cdot 1}=\frac{5}{\sqrt{93}}[/m]
[m]∠ (EFP,ABCD)= ∠ (\vec{n_{1}}, \vec{n_{2}})=arccos \frac{5}{\sqrt{93}}[/m]