Задача 75262 На ребре SB тетраэдра SABC отметили...

659cc09d9ae5ec093245471a

1/9/2024 3:43:39 AM

На ребре SB тетраэдра SABC отметили точку К так, что SK: KB = 3 : 2. Известно, что AB = AC, SB = SC = 13 см, ВС = 24 см. Найдите расстояние между прямыми АК и ВС

5f3ea7e3faf909182968ddd9

1/9/2024 6:07:22 AM

★

Прямые АК и ВС - скрещивающиеся
Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной прямой
до плоскости, проходящей через вторую прямую параллельно первой.

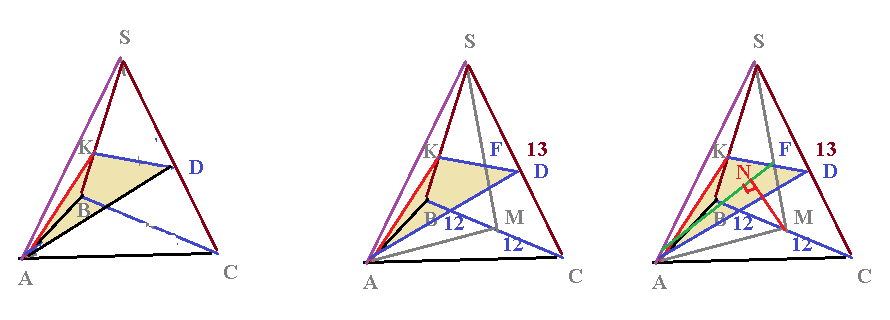
Поэтому проводим через точку К прямую KD, параллельную BC.

KD || BC
(AK=AD)

Проводим
SM ⊥ BC
SM- высота, медиана и биссектриса равнобедренного треугольника ВSM
ВM=MC=12
BM=sqrt(13^2-12^2)=5

Пусть F- точка пересечения KD и BM
AF- медиана и высота равнобедренного треугольника AKD.

MN ⊥ AF
MN - [i]искомое расстояние[/i]


Из подобия Δ SKF и Δ SBM
SF=3
FM=SM-SF=5-3=2

В прямоугольном треугольнике MNF найден только один элемент
Этого недостаточно.



Δ MNF ∼ Δ AFM

Но в Δ AFM неизвестны стороны...

В условии АВ=АС = ???