Задача 66542 ...

634ed79e18664a754e4e33f1

27.10.2022 22:19:49

Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом 45° до площини основи. Знайдіть площу поверхнi призми, якщо площа перерізу 4√3 см².

5f3ea7e3faf909182968ddd9

28.10.2022 10:07:16

★

В основании призмы равносторонний треугольник со стороной [b]а[/b]
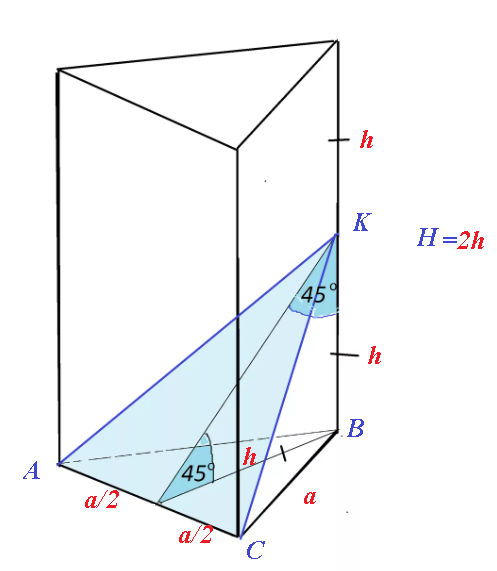
Высота ВМ такого треугольника является одновременной и медианой,
AM=MC=a/2

BM=asqrt(3)/2

h=asqrt(3)/2

ВМ ⊥ AC
KM ⊥ AC

∠ КМВ- линейный угол двугранного угла
∠ КМВ=45 °

Δ КМВ - прямоугольный[b] равнобедренный[/b]

КB=BM=asqrt(3)/2 ⇒

По теореме Пифагора

KM^2=KB^2+BM^2

KM^2=(asqrt(3)/2)^2+(asqrt(3)/2)^2

KM^2=a^2*(3/4)+a^2*(3/4)

KM^2=(3/2)a^2

S_(cечения)=S_( Δ AKC)=(1/2)*AC*KM=(1/2)*a*(a*sqrt(3/2)=a^2sqrt(3)/2sqrt(2))

По условию

S_(cечения)=4sqrt(3)


a^2sqrt(3)/2sqrt(2))=4sqrt(3) ⇒ [red]a^2=8sqrt(2)[/red]


H_(призмы)=2KB=[blue]a*sqrt(3)[/blue]

S_(бок. призмы)=P_(осн)*Н= 3а*[blue] a*sqrt(3)[/blue]=3a^2*sqrt(3)=3*([red]8sqrt(2)[/red])*sqrt(3)=...