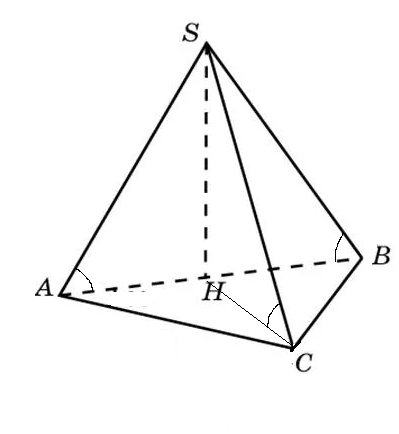
Задача 60344 В основании пирамиды лежит прямоугольный...

60dc14daa1c50e1d30441803

30.06.2021 09:54:16

В основании пирамиды лежит прямоугольный треугольник с катетами 6 и 8. Объём пирамиды равен 40. Все боковые рёбра наклонены к плоскости основания под одинаковым углом, Найдите этот угол.
Выберите один ответ:

a. 65°

b. 45°

c. 75°

d. 30°

e. 60°

5f3ea7e3faf909182968ddd9

30.06.2021 12:41:34

★

В основании пирамиды лежит прямоугольный треугольник с катетами 6 и 8.

AC=8
BC=6

Все боковые рёбра наклонены к плоскости основания под одинаковым углом

∠ SAH=∠ SBH=∠ SCH

SH ⊥ пл. АВС

Δ SAH=Δ SBH=Δ SCH по катету SH и острому углу.

⇒ SA=SB=SC

AH=BH=CH ⇒ H - равноудалена от вершин треугольника, значит точка Н - центр описанной окружности.

В прямоугольном треугольнике гипотенуза - диаметр описанной окружности.

Значит H - середина гипотенузы АВ.

По теореме Пифагора

AB^2=AC^2+BC^2=8^2+6^2=64+36=100

AB=10


AH=BH=CH=5


S_(осн)=S_Δ ABC)=(1/2)*AC*BC=(1/2)*8*6=24


V_(пирамиды_ = 1/3 S_(осн)*h,

где h - высота пирамиды,S - площадь основания

⇒

h=3V_(пирамиды)/S_(осн)=120/24=[b]5[/b]


Δ SAH=Δ SBH=Δ SCH - прямоугольные равнобедренные

AH=BH=CH=[b]5[/b] и SH=h=[b]5[/b]



∠ SAH=∠ SBH=∠ SCH=45 °