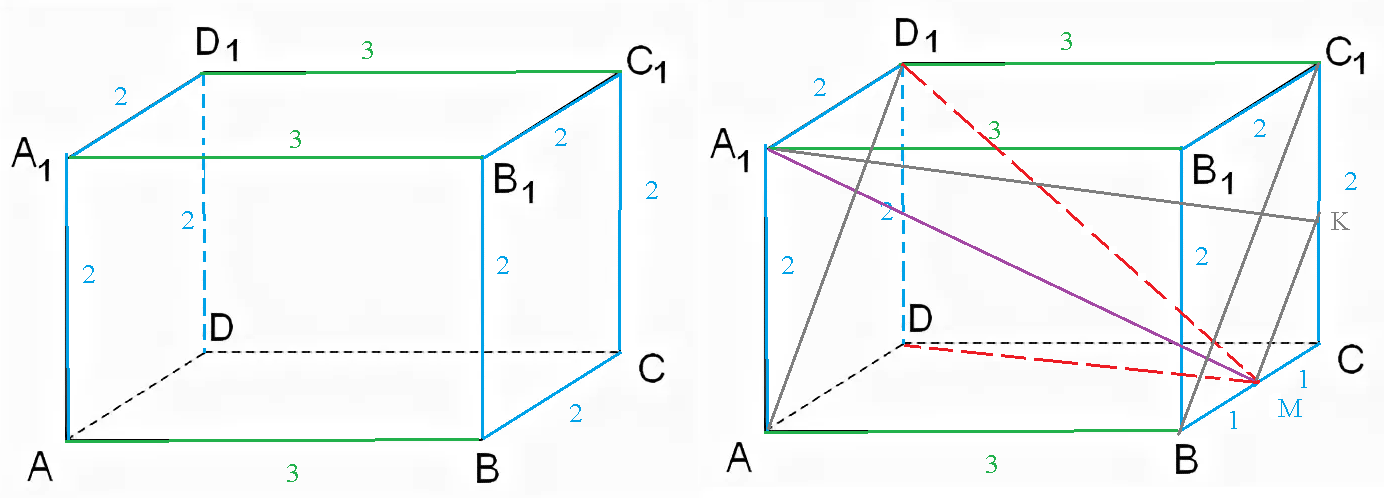
Задача 59679 В прямоугольном параллелепипеде...

609a4f5c948cd266b38ee0ac

11.05.2021 12:34:48

В прямоугольном параллелепипеде ABCDA1B1C1D1
BC=AA1=2, AB=3, точка M- середина BC.
Найти:
а) длину отрезка MD1
б)угол между A1M и AD1
в)расстояние от точки D до плоскости B1AM
г)угол между DM и плоскостью B1AM
д)угол между плоскостями B1AM и ACD1

5f3ea7e3faf909182968ddd9

11.05.2021 13:51:18

★

а) MD^2_(1)=MD^2+DD^2_(1)

MD^2=MC^2+CD^2=1^2+3^2=10

MD^2_(1)=10+2^2=14

MD_(1)=sqrt(14)


б)угол между A1M и AD1

BC_(1) || AD_(1)

MK||BC_(1)

угол между A1M и AD1 равен углу между A1M и MK

Это угол А_(1)MK

Рассмотрим Δ А_(1)MK

А_(1)М=А_(1)К=sqrt(14) ⇒ Δ А_(1)MK равнобедренный

MK=sqrt(2)

косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе

cos ∠ А_(1)MK=(1/2)MK/A_(1)M=sqrt(2)/(2sqrt(14))=1/(2sqrt(7))




в)расстояние от точки D до плоскости B1AM
г)угол между DM и плоскостью B1AM
д)угол между плоскостями B1AM и ACD1