Задача 65271 На рисунке угол между прямым...

61ec3a315ad3fc21df932eba

02.07.2022 13:52:37

На рисунке угол между прямым шестиугольным празманом 2 единицами CE' и векторами DF.

5f3ea7e3faf909182968ddd9

02.07.2022 16:01:57

★

Если найти угол между векторами vector{CE'} и vector{BF}, то это угол между
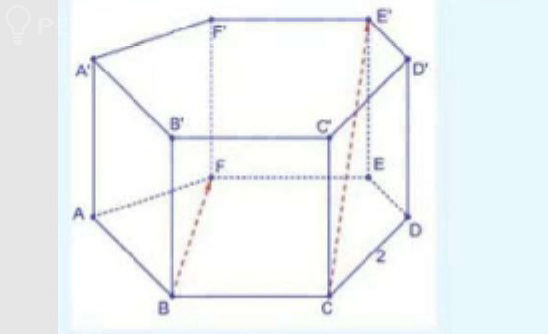
vector{CE'} и vector{CE}, который равен vector{BF}

Находим угол из прямоугольного треугольника СЕЕ`

tg ∠ ЕCЕ`=EE`/CE

CE^2=CD^2+ED^2-2CD*ED*cos120 ° =2^2+2^2-2*2*2*(-1/2)=12

CE==2sqrt(3)

tg ∠ ЕCЕ`=2/2sqrt(3)

tg ∠ ЕCЕ`=1/sqrt(3)

∠ ЕCЕ`=30 °