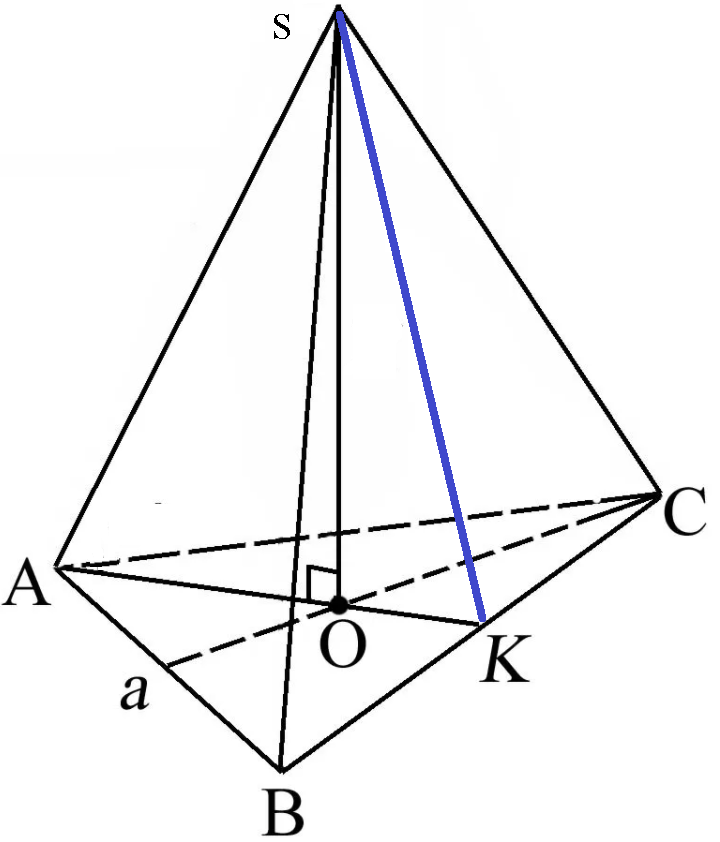
Задача 60791 Сторона основания правильной треугольной...

608450e4031948747667d928

20.09.2021 19:32:47

Сторона основания правильной треугольной пирамиды равна 12 см, а высота-2 см. Найдите апофему пирамиды. Подробно с объяснениями.

5f3ea7e3faf909182968ddd9

20.09.2021 20:45:51

★

Пирамиды - правильная ⇒ В основании правильный треугольник, т.е равносторонний.

АВ=ВС=АС=12 см.

SO ⊥ плоскости АВС

SA=SB=SC- боковые ребра правильной пирамиды.

Это наклонные

Равные наклонные имеют равные проекции

ОА=ОВ=ОС

О- центр описанной окружности и О- центр вписанной окружности

В правильном треугольнике они совпадают

В правильном треугольнике

R=asqrt(3)/3 - радиуc окружности, описанной около треугольника со стороной а

r=asqrt(3)/3 - радиуc окружности, вписанной в правильный треугольник со стороной а

а=12,

значит R=12sqrt(3)/3=3sqrt(3)

r=12sqrt(3)/6=2sqrt(3)


ОА=ОВ=ОС=R=3sqrt(3)

ОК=2sqrt(3)

SO=2

По теореме Пифагора из треугольника SOK

SK^2=SO^2+OK^2=4+12=16

SK=4