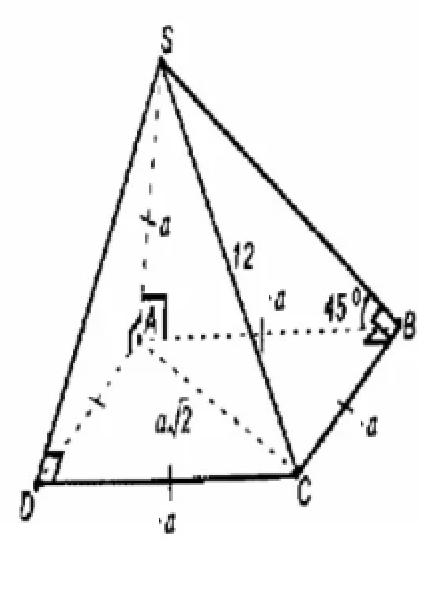
Задача 67994 Основанием пирамиды является квадрат,...

63aaf68bbcce014be7521da4

28.12.2022 00:07:11

Основанием пирамиды является квадрат, одна из боковых рёбер перпендикулярна плоскости основания. Плоскость боковой грани, не проходящей через высоту пирамиды наклонена к плоскости основания под углом 45°.Наибольшее боковое ребро 12 см. Найдите высоту пирамиды.

5f3ea7e3faf909182968ddd9

28.12.2022 11:44:00

★

Пусть сторона квадрата равна [b]а[/b]

Тогда
АС [b]a [/b] sqrt(2) - диагональ квадрата

Плоскость боковой грани, не проходящей через высоту пирамиды наклонена к плоскости основания под углом 45°.

Это плоскости SCD и SBC

Так как
SA ⊥ пл АВСD ⇒ SA ⊥ AB
AB ⊥ BC

BC ⊥ пл SAB ⇒ BC ⊥ SB

∠ SBC=90 °

∠ SBA=45 ° - линейный угол двугранного угла между SBA и АВСD
(AB ⊥ BC и SA ⊥ BC)

Δ SBA - прямоугольный, с острым углом 45 ° ⇒ Δ SBA - равнобедренный прямоугольный ⇒

SA=AB=[b]a[/b]


SA ⊥ пл АВСD ⇒ SA ⊥ AC

Δ SCA - прямоугольный

По теореме Пифагора

SA^2+AC^2=SC^2

[b]a[/b]^2+([b]a[/b]*sqrt(2))^2=12^2

3[b]a[/b]^2=144

[b]a[/b]^2=48

[b]a[/b]=4sqrt(3)


SA=H_(пирамиды)=[red]4sqrt(3)[/red]