Задача 57585 Дан куб с ребром, равным 1. Найдите...

6016d24b5d2ce76e3c5699c4

31.01.2021 18:56:13

Дан куб с ребром, равным 1. Найдите синус угла между прямой В1D u (ABC1).

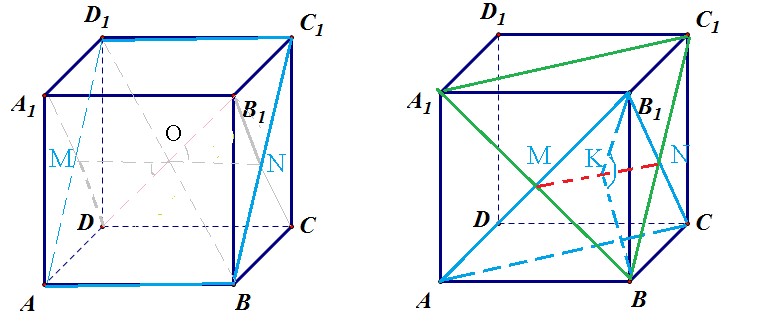
Дан куб с ребром, равным 1. Найдите синус угла между (АВ1С) и (А1ВС).

5f3ea7e3faf909182968ddd9

31.01.2021 23:47:04

★

1.
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость.

MN- проекция B_(1)D на пл. АВС_(1)D_(1)

MN|| DC

∠ B_(1)DC - искомый угол находим из Δ В_(1)DC по теореме косинусов.

B_(1)D=sqrt(3)
B_(1)C=sqrt(2)
DC=1

DC^2=B_(1)D^2+B_(1)C^2-2*B_(1)D*B_(1)C*cos∠ B_(1)DC ⇒

cos∠ B_(1)DC=(B_(1)D^2+B_(1)C^2-DC^2)/(2*B_(1)D*B_(1)C)=2/sqrt(6)

2.
Две плоскости АВ_(1)С и А_(1)ВС имеют две общие точки: M и N.

Значит пересекаются по прямой, проходящей через эти точки:

MN || AC
MN=AC/2=sqrt(2)/2

Δ MB_(1)N и Δ МВN - равносторонние равные между собой треугольники со стороной sqrt(2)/2

B_(1)K=BK=(sqrt(2)/2)*sqrt(3)/2 - высоты равносторонних треугольников со стороной sqrt(2)/2

∠ B_(1)KB - линейный угол двугранного угла между плоскостями АВ_(1)С и А_(1)ВС

По теореме косинусов из Δ B_(1)KB:

B_(1)B^2=B_(1)K^2+BK^2-2*B_(1)K*BK*cos ∠ B_(1)KB ⇒

cos ∠ B_(1)KB =[b]-1/3[/b]