Задача 65263 Грани abcda1b1c1d1 равны 1 см. Найдите...
Условие
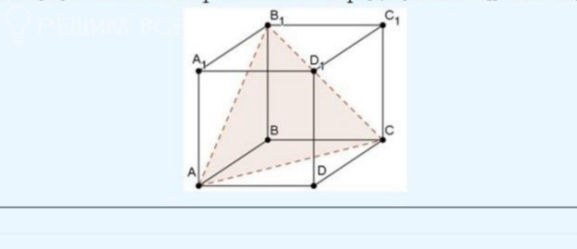
Решение
Угол между прямой и плоскостью - угол между прямой и ее проекцией на плоскость
Проекцией B_(1)D на плоскость является B_(1)O
Δ АВ_(1)С - равносторонний
AC=BD=АВ_(1)=В_(1)С=sqrt(2)
AO=AC/2=sqrt(2)/2
B_(1)O^2=АВ^2_(1)-AO^2=(sqrt(2))^2-(sqrt(2)/2)^2=3/2
B_(1)O=sqrt((3/2))
Из прямоугольного треугольника BB_(1)O
sin∠ BOB_(1)=BB_(1)/B_(1)O=1/sqrt((3/2))=sqrt(2/3)
B_(1)D=BD_(1)=sqrt(3)
Δ ВКЕ ∼ Δ B_(1)KD_(1)
BK:KD_(1)=B_(1)D:BO=1:(1/2)=2:1 ⇒ BK=(1/3)B_(1)D=sqrt((3))/3
По теореме синусов для треугольника ВКО
ВК:sin ∠ BOK=BO:sin ∠ BKO
⇒
sin∠ BKO=BO*sin∠ BOK/BK=(sqrt(2)/2)*(sqrt(2/3))/(sqrt((3))/3)=sqrt(2/3)