Задача 56400 плоскость y параллельная оси цилиндра...
Условие
Решение
ОО_(1) ⊥ плоскостям оснований ⇒
AB ⊥ плоскостям оснований ⇒ AB ⊥ любой прямой лежащей в этих плоскостях в том числе:
AB ⊥ ВС
АВ ⊥ AD
CD ⊥ плоскостям оснований ⇒ CD ⊥ любой прямой лежащей в этих плоскостях в том числе:
CD ⊥ ВС
CD ⊥ AD
AB|| CD
AB=CD
AB ⊥ ВС
CD ⊥ ВС
ABCD- параллелограмм все углы которого прямые, значит АВСD -прямоугольник
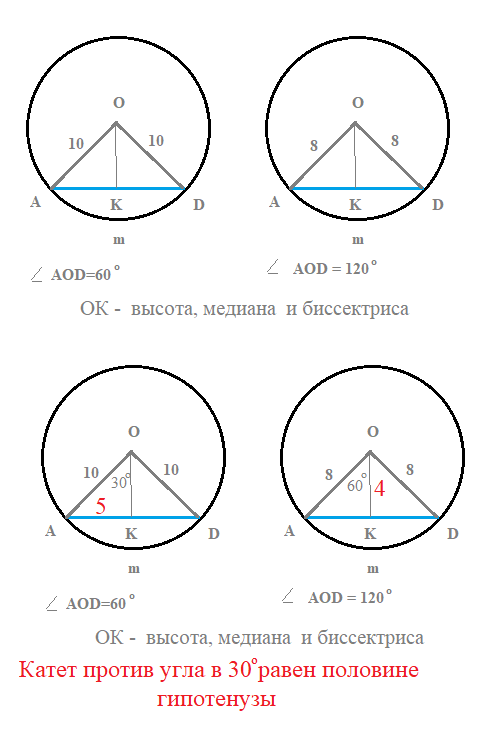
2. см рис
1 вариант
AK=5
AD=2AK=2*5=[b]10[/b]
или потому, что треугольник AOD - равнобедренный, с углом при вершине 60 °
Значит и углы при основании по 60 °
треугольник AOD - равносторонний: AO=OD=AD=[b]10[/b]
2 вариант
ОК=4
AK^2=AO^2-OK^2=8^2-4^2=64-16=48
AK=sqrt(48)=4sqrt(3)
AD=2AK=2*4sqrt(3)=[b]8sqrt(3)[/b]
или
sin ∠ AOD=AK/AO
∠ AOD=60 ° ⇒
AK=AO*sin60 ° =8*sqrt(3)/2=4sqrt(3)
AD=2AK=2*4sqrt(3)=[b]8sqrt(3)[/b]