Задача 65190 Висота правильної трикутної піраміди...

62b2bbab58e429228ad172cf

22.06.2022 09:51:22

Висота правильної трикутної піраміди дорівнює 6 см, а кут, який утворює апофема з площиною основи піраміди, дорівнює 30°. Обчисли об'єм піраміди.

5f3ea7e3faf909182968ddd9

22.06.2022 12:32:59

★

SO- высота пирамиды

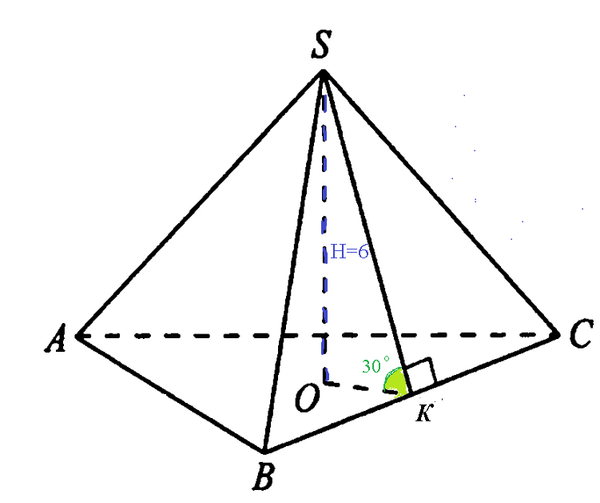
SO ⊥ плоскости АВС ⇒SO ⊥ любой прямой в этой плоскости

SO ⊥ OK

Угол между прямой и плоскостью это угол между прямой и ее проекцией на плоскость.

ОК- проекция SK

∠ SKO=30 °

Катет против угла в 30 ° равен половине гипотенузы

SK=12 ( гипотенуза в 2 раза больше этого катета)

Тогда по теореме Пифагора

OK^2=SK^2-SO^2=12^2-6^2=144-36=108

OK=sqrt(108)=\sqrt(36*3)=sqrt(36)*sqrt(3)=6sqrt(3)


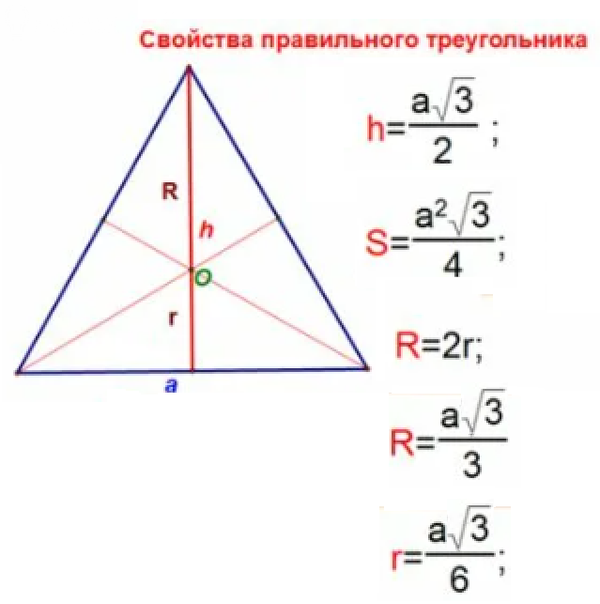
OK=r - радиус окружности вписанной в треугольник АВС

a- сторона равностороннего треугольника АВС

Тогда

r=asqrt(3)/6 ⇒ [b]a[/b]=2sqrt(3)*r=3sqrt(3)*6sqrt(3)=18*3=[b]54[/b]



S_( Δ ABC)=54^2sqrt(3)/4

V=(1/3)S_( Δ ABC)* H=(1/3)*(54^2sqrt(3)/4)*6=... считайте.