Задача 57554 Из точки лежащей вне плоскости проведены...

601517d55d2ce76e3c56932f

30.01.2021 11:25:01

Из точки лежащей вне плоскости проведены к этой плоскости две наклонные и перпендикуляр.Определите длину перпендикуляра, если наклонные равны 13см и 15 см, а разность их проекции равна 4 см

5f3ea7e3faf909182968ddd9

30.01.2021 11:52:15

★

Пусть АВ- перпендикуляр, наклонные AD и AC

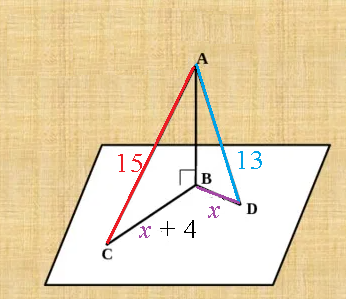
AD=13

AC=15

Б[red]о[/red]льшая наклонная имеет и б[red]о[/red]льшую проекцию

BD- проекция AD

BC- проекция AС

По условию разность проекций равна 4 см

Пусть BD=x
Тогда АС=x+4


AB^2=15^2-(x+4)^2
AB^2=13^2-x^2

Приравниваем правые части и получаем уравнение:

15^2-(x+4)^2=13^2-x^2

15^2-13^2=(x+4)^2-x^2

(15-13)*(15+13)=(x+4-x)*(x+4+x)
2*28=4*(2x+4)

2х+4=14
2х=10
х=5 - проекция

х+4=9 - проекция

АВ^2=13^2-9^2=169-5^2=169-25=144

AB=12