Решение тригонометрических уравнений

Решение уравнений .

а) решите уравнение 2sin(2x+π/6)-2sqrt(3)cosx=sqrt(3)sin2x+7/2
б) найдите все корни уровнения принадлежащие отрезку [3π;9π/2]

а)решите уровнение 0,5cos2x-cosx +2cos^(3)x=0
б)найдите корни уравнения принадлежащие отрезку [-1,5π;0,5π]

а) решите уравнение 5sinx×cosx+14cos^(2)x=0
б) укажите корни этого уравнения принадлежащие отрезку [π;2π]

а) решите уравнение tg(π-x)cos(3π/2-2x)=sin 5π/6
б) укажите корни этого уровнения принадлежащие отрезку [-2π;-π/2]

а) решите уравнение 2cos^(3)x +3cos^(2)x+cosx/sqrt(ctgx)=0
б)найдите все корни этого уравнения принадлежащие промежутку [-2π;-π/2]

а) найдите корень уровнения ctg^(3)x-ctgx/sqrt(cosx)=0
б)найдите все корни этого кравнения принадлежащие отрезку [-2π;-π/2]

а) решите уравнение sqrt(3)tgx+1/2sinx-1=0
б)найдите все корни этого уравнения принадлежащие этому отрезку [9π/2;6π]

а) решите уравнение (1-3tg^(2)x)sqrt(7sinx)=0
б)найдите все корни этого уранения принадлежащие отрезку [-2π;-π/2]

Решите уравнение:
(√2sin(x/2)-√2cos(x/2))^2=5+sin(pi/4-x/2)

2 cos^2 (3π/2 + x) = sin 2x [ -9π/2 , -3π ]

а)решите уравнение 2cos(P/2-x)=tgx
б)[-2p;-p/2]

1)решите уравнение sin2x/cos(x+3п/2)=1
2)найдите корни принадлежащими этому отрезку [-4п;-5п/2]

a) Реши уравнение (sin x - 1) * (2 cos x - 1) / sqrt(tgx) = 0.

b) Укажи корни данного уравнения, принадлежащие отрезку [-π, π].

а) Решить уравнение sin2x / sin(3π/2–x) = √2

б) Отбор корней на отрезке [2π; 7π/2] решить с помощью неравенства

Напишите градусную меру угла а,который образует ОА с положительной полуосью Ох

2cos(2x-pi/3)-sinx=корень из 3sin2x

а) решите уравнение 4sin^(3)=3cos(x-п/2)
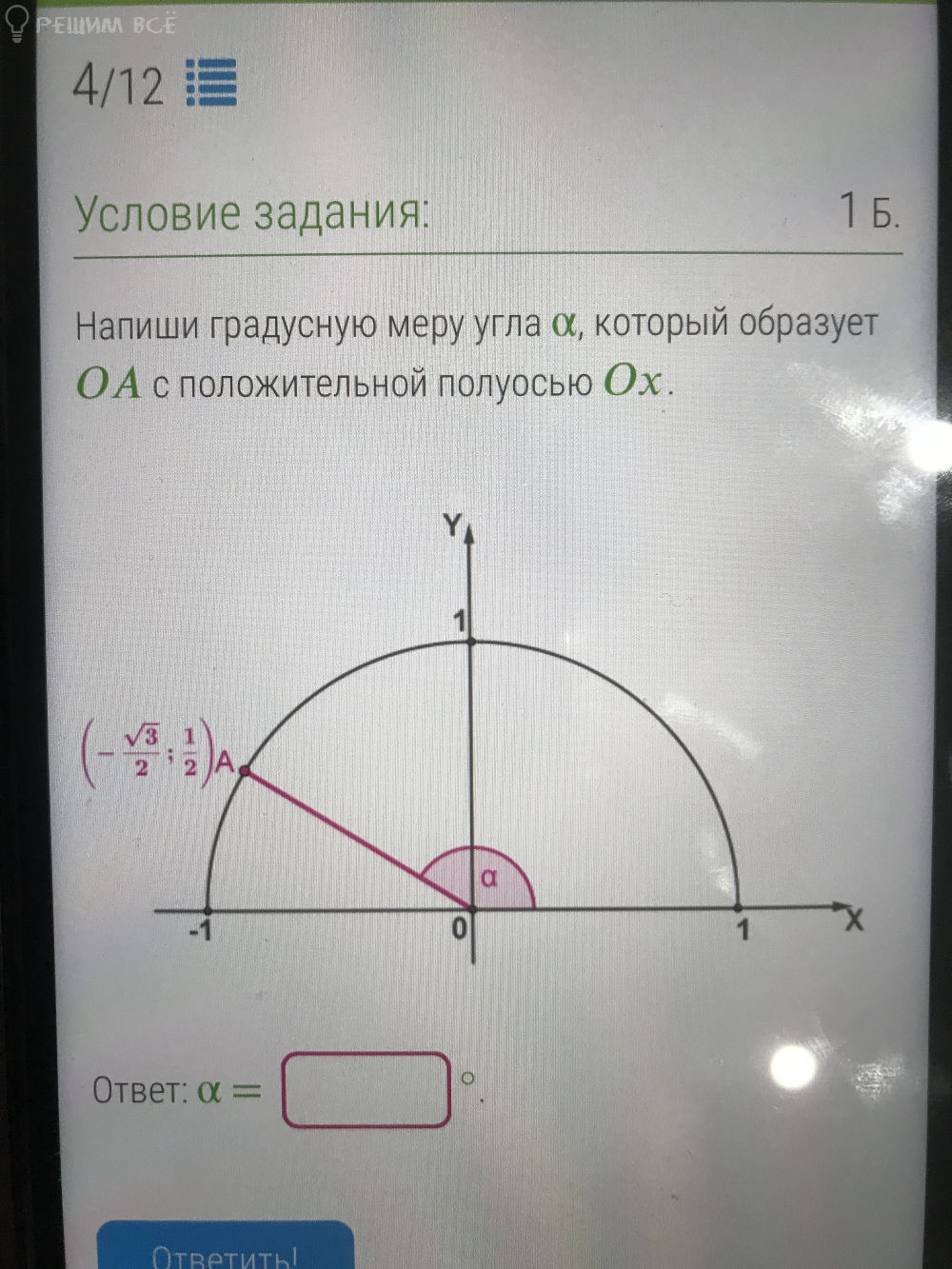
б) найдите все корни этого уровнения, принадлежащие отрезку [7п/2;9п/2]

а) решите уравнение sin2x=√2cos(п/2+x)
б) найдите все корни этого уровнения, принадлежащие отрезку [–2п;–п]

С помощью графика функции y=cos x найти корни уравнения, принадлежащие данному промежутку
cos x = - 1/2, [-п/2;п]

С графиком

Сколько корней имеет уравнение. Можно с решением.

cos3x×cos4x-sin3x×sin4x=½

sinx+sin3x=0

Sinxcos5x-sin9xcos3x=0

cos²(7π+x)=1/2

Решение этого примера

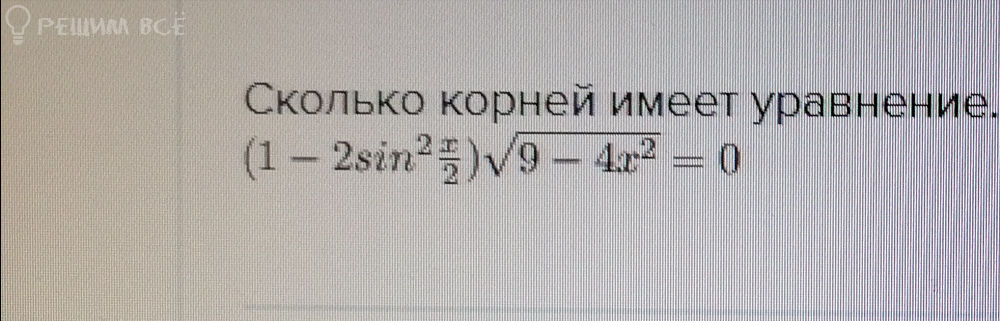
sqrt(2tg(3Pi/2 - x)sin(3Pi-2x)) = -tg(2Pi/3)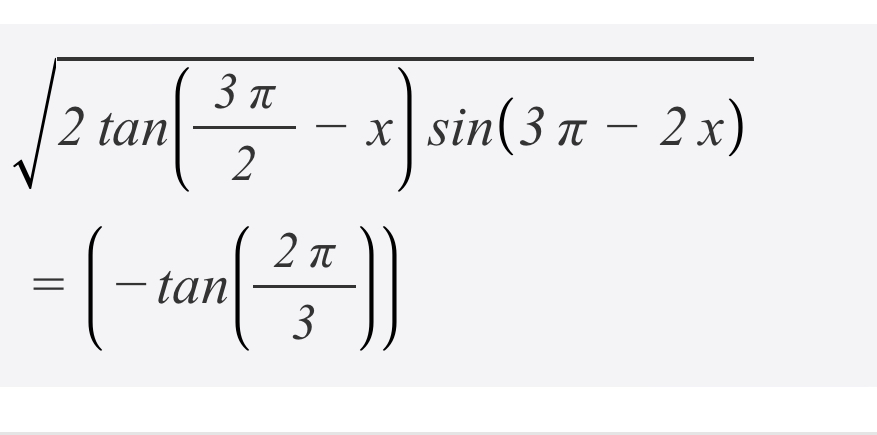

cos(x/2)*sin(3x/2)=4*sin^(2) (π+x)*cos^(2) (π-x)-sin(x/2)*cos(3x/2), если при условии [π; 3π]

Сколько корней имеет уравнение : (1-2sin^2(x/2))sqrt(4-x^2)=0

2cos^(2)x+2cosx+sin2x=0 [π;3π]

Решите уравнение cosx-cos2x = sin3x

2cosx^2+cosx-1=0 [-7p/2;-2p]

sin πx/3=-1

Решить уравнение:
[block](4sin^4x+3cos2x-1)/(sqrt(tgx)) = 0[/block]

Найти все корни уравнения на отрезке [3π/2; 3π].

Найти сумму корней в градусах уравнения cos x - 2sqrt(3)sin^2 x = cos 3x принадлежащих отрезку [0; 360]

Решить уравнение — 2соs4хcosx+З(cos^22x-sin^22x) =0. В ответе указать наименьшее положительное решение в градусах.

sinx-2sin2x+sin3x= (1-2cosx+cos2x)

Решить уравнение и найти корни принадлежащие промежутку

13. а) Решите уравнение sqrt(3)(cos4x+1) = 2(2-cos4x)cos2x

Решите
а) 2· (cos2x)^2 – 4·(cos2x)^2 ·(sinx) ^2=sin(2x–p/2)
б) [0;p]

Решите уравнение
sinx-cosx=√2 , если х є [0;π]

2sin^2x=2+sqr3*sin2x

Решить уравнение
2sin^2x+1=2sqrt2sin(3pi/2+x)
Найти корни уравнения на промежутке: [17pi; 37pi/2]

Решите уравнение

1+sinx+cosx = 2cos(x/2 - 45)

Помогите Пожалуйста!!! Найдите частичное решение уравнения
2( tgx-ctgx)=√3•(tg²x+ctg²x)-2√3

√3cos^x=sinx cosx

Помогите пожалуйста!!!Решите уравнение
2 cos πx/2=√(x²-8x+20)

Помогите Пожалуйста!!!!Найдите частичное решение уравнения tg²x+ctg²x-3(tgx+ctgx)+4=0
А) -π/4
Б)π/6
В)π/3
Г)3π/4
Д)π/4
Один ответ!

а) Решите уравнение tg(Pi-x)cos(3Pi/2 - 2x) = sin 5Pi/6

б) Укажите корни этого уравнения, принадлежащие отрезку [-2Pi; -Pi/2]

1. Упростите выражение cos2????+sin2????∙tan????+cos????.
2. В одной и той же системе координат на отрезке [0;2????]постройте графики функций ????(????)=cos???? и ????(????)=cos2???? и найдите абсциссы точек пересечения графиков функций.
3. При помощи чертежа пункта 2. на отрезке [0;2????]найдите значения аргумента х при которых ????(????)<????(????)

Решите уравнение sin(2x + 2π/3) cos(4x + π/3) - cos 2x = sin²x / cos(-π/3).

Решить уравнение sin(x)+sin^2(x)+cos^3(x)=0

sinxcos5x-sin9xcos3x=0

Решить уравнение (tgx)^4+(ctgx)^4+(tgx)^2-(3/4)*(ctgx)^2=2

2cosx^2-2cos2x^2+2cos3x^2=1

Найдите значение выражения 25^(log_5√17).

Решите уравнение (2 cos x - √3) * log_6(- tg x) = 0.

Решить и расписать решение, спасибо!

tgx*ctgx/2+ctgx/2=0

Решите sin9x+13sin3x=0

Решите пожалуйста!!! 2sin^2x-15sinxcosx-8cos^2x=0

уравнение cos^2 5x+cos^2 3x=1

sin5x*cos3x-cos5x*sin3x=-0,5

Помогите пожалуйста! 2sin^22x=3cos2x

2sin^2x+2cosxsin^2x-sin^2x-sinxcos^2x-cos^3x=0

3) sin² 3x = cos² 3x;

4) sin x/2 + cos x = 1.

Срочнооо
!!!!Решите tg^4x-4tg^2x+3=0 и найдите количество корней на интервале (0; п)

а) Решите уравнение:

[m] \sqrt{2} \sin^3 x - \sqrt{2} \sin x + \cos^2 x = 0. [/m]

б) Найдите все корни этого уравнения, принадлежащие отрезку [m] \left[ -\frac{5\pi}{2} ; -\pi \right] .[/m]

6cos^(2)x - 7cos(3π/2-x)-1=0 [2π ; 7π/2]

Помогите пожалуйста решить номер 3.54

а) Решите уравнение tg8x-tg3x=sin5x
б) найдите все корни уравнения на отрезке [-п/2;п]

2cos^2(x)+sinx-2=0

4sin2x=tgx, [–π;0]

Решите уравнение.
Sin^2 x+2sinx cosx=1

Решите уравнение arcsin3x = π/3

sinx+cosx = 2sqrt(2)sinx*cosx

13 задание профиль
уравнение равняется 0

13 задание профиль

Решите уравнение:
cos2 х-8 cos х+3=0

Решите уравнение [m]tg^{4}x-4tg^{2}x+3=0[/m]
И найдите корни этого уравнения, принадлежащие отрезку [2π;[m]\frac{7π}{2}[/m]]

a) Решите уравнение 15^(cos x) = 3^(cos x) ⋅ 5^(sin x);

б) Найдите все корни этого уравнения, принадлежащие отрезку [5π; 13π/2].

Решите уравнение
(2cos^2x + 11cosx + 5) · log(18)(sinx) = 0.

Решите уравнение 2 cos³ x = sin (π/2 - x) + 0,5 sin 2x.

Срочно нужна помощь. Математика профиль 13 задание

√3 sin x + cos x = 0

5 sin x + 3 cos x = 0

sin² x + 3 sin x cos x - 4 cos² x = 0

5 sin² x - 17 sin x cos x + 4 cos² x + 4 = 0

sin³ x - sin² x cos x - 3 sin x cos² x + 3 cos³ x = 0

^(2sin)x-sqrt(3)sin2x=0 помогите решить уравнение!

a) (log^2_3(tg^2 x) - 2log3(tg x)) / (sqrt(2 cos x + 1)) = 0.
б) [-π; π/2] .

1.Найдите все значения x и y , удовлетворяющие уравнению :
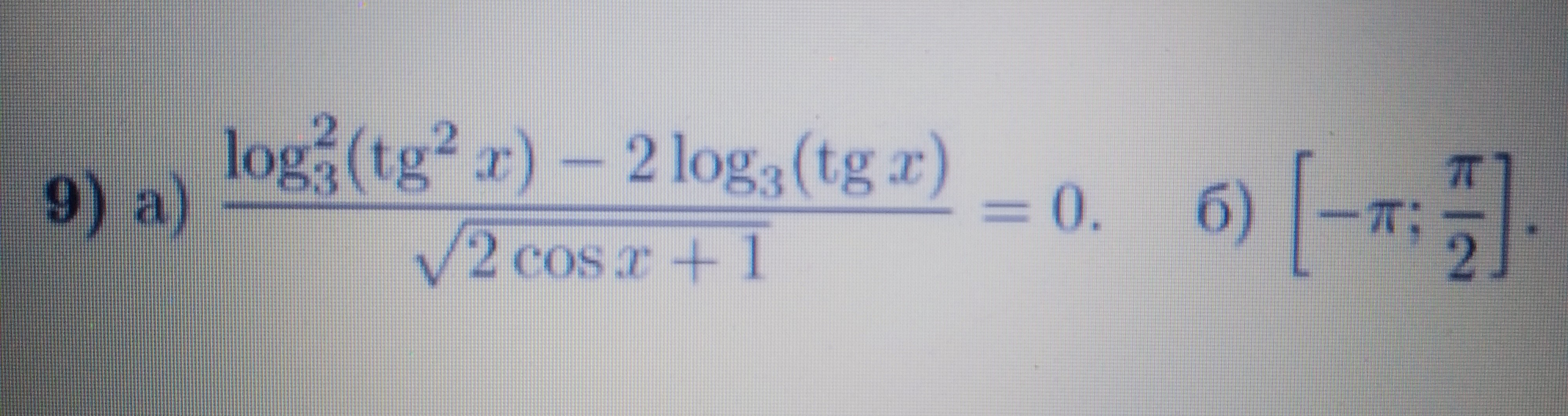
12sin x + 5cos x=2y^2-8y+21
2.Вычислите:
cos^4α+ sin^4α , если sin 2α=2/3

№ 4.41

tg 14x + 3 ctg 7x + sin 3x - 2√2 sin(3x/2 + Pi/4) = 4/(sqrt(3)+1)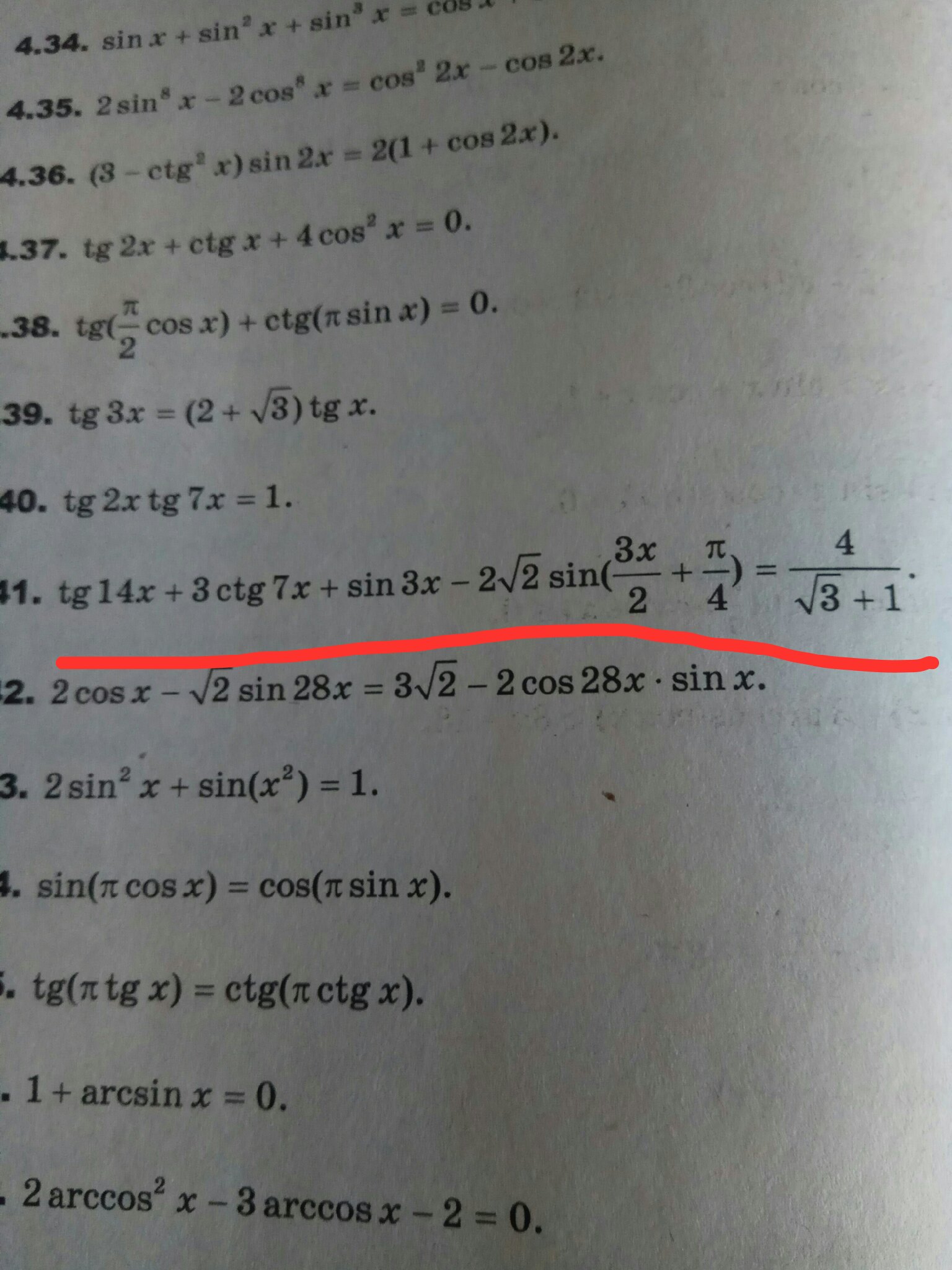

[m]\frac{4cos^2x-3}{\sqrt{\frac{1}{3}-sinx}}=0[/m]

[m]\left[ \frac{\pi}{6}, 3\pi \right)[/m]

Помогите решить адание д) и е) подробное решение

Решить уравнение:
[m]\frac{4cos^2x-3}{\sqrt{\frac{1}{2}-sinx}}=0[/m]

Подскажите пожалуйста, как найти одз в этом номере!

|ctg(2x-π/2)| = 1/(cos^(2)2x) -1

sin(п+x)*sin(2x-3п/2) = 1

tg2x=4cos^2 x-ctgx

С 379 номера и до конца)))

5sin^2x-14sinxcosx-3cos^2x=2

Решите уравнение 2sin2x = sinx - sqrt(3)cosx.

sin 2x + cos 2x + sin x + cos x + 1 = 0

Решите тригонометрические уравнения

4.4.12
cos7x - sin 5x =√3(cos5x - sin7x)
0<x<30°

4.4.15
(sinx +√3 cosx)^2-5 = cos(Pi/6 - x)

4.4.1
cos 3x + sin 3x = √2, [7Pi/4; 9Pi/4]


4.4.4
1 + cos 2x + sin 2x = 0

Решите тригонометрические уравнения

4.2.22.

8sin^4x+13cos2x = 7
270 < x < 360

4.2.28.

tgx-5tg(x-5Pi/2) = 6sin(13Pi/2)
Pi ≤ x ≤ Pi

а)cos2 x +3cos(3π/2+x)-2=0
б)[-5π;-3π]

Решить уравнение:
√( 3 sin0,25x - 4)² - √( sin² 0,25x - 6 sin0,25x + 9) = 1 -√2

a) Решите уравнение 4sin^3x = cos(x - 5π/2).

б) Укажите корни этого уравнения, принадлежащие отрезку [3π/2; 5π/2].

√2 sin x + cos^2 x = √2 cos^3 (x - Pi/2)

Срочно нужна ваша помощь

2cos^3x-cos^2x+2cosx-1=0 2pi 7pi/2

a) Решите уравнение [m]3\sqrt{3}cos\left(\frac{3\pi}{2} + x\right) - 3 = 2sin^{2}x[/m].

б) Укажите корни этого уравнения, принадлежащие отрезку [m][2\pi; 3\pi][/m].

а) Решите уравнение 8sinx+4cos^2x = 7;

б) Найдите корни на отрезке [-3Pi/2; -Pi/2]

Добрый вечер! Пожалуйста решите подробно 3tgx-2ctgx-5=0

решить уравнение
(sin2x-1)(cos^2x-1)=0 и найти все его корни на промежутках: а)(0,2π). б) (-2π,0)
в) (-π/2,π). г) (4π, 11π/2)

Уравнения:
[b]1.[/b] 2sin x/2=1-cosx

[b]2.[/b] cos(3π/2+x)cos3x-cos(π-x)sin3x= -1

sin^2(7π/2+x)-sin2x=0

3. 4cos(x/4 + Pi/6) = sqrt(3)

4. [m]\frac{2sinx+\sqrt{3}}{2cosx+1} =0[/m]

[block](2cosx+sqrt(2))/(2sinx+sqrt(2)) = 0[/block]

[block](sin4x)/(cos4x-1) = 0[/block]

7. cos(x/2 - π/12) · (sin(x - π/3) + 1) = 0

8. (cos4x + 1)(sin2x - 1) = 0

5. sin^2x-6sinx = 0

6. cos6x+cos4x = 0

7. sin2x-2sinx = 0

8. 3sin2x+2sin^2x = 0

9. 7cos2x+18sin^2x-9 = 0

10. cos2x+11sinx-6 = 0

11. 11sin2x+32sin^2x-12 = 0

12. 5cosx-10sinx-11 = 0

Создатель