Задача 55422 ...

5f282cfba9074b3a3bc0f013

07.11.2020 20:41:21

4sin2x=tgx, [–π;0]

5f3ea7e3faf909182968ddd9

07.11.2020 21:04:01

★

[m]4\cdot sin2x=tgx[/m]

так как [m] tgx=\frac{sinx}{cosx}[/m]

[m]4\cdot sin2x=\frac{sinx}{cosx}[/m]

[m]4\cdot sin2x-\frac{sinx}{cosx}=0[/m]

[m]\frac{4\cdot sin2x\cdot cosx-sinx}{cosx}=0[/m]

[m]\left\{\begin{matrix}
4\cdot sin2x\cdot cosx-sinx=0\\cosx ≠ 0 \end{matrix}\right.[/m]

[m]\left\{\begin{matrix}
4\cdot sin2x\cdot cosx-sinx=0\\cosx ≠ 0 \end{matrix}\right.[/m]

так как [m] sin2x=2\cdot sinx\cdot cosx[/m]

[m]\left\{\begin{matrix}
4\cdot 2\cdot sinx\cdot cosx \cdot cosx-sinx=0\\cosx ≠ 0 \end{matrix}\right.[/m]

[m]\left\{\begin{matrix}
sinx \cdot (8\cdot cos^2x -1)=0\\cosx ≠ 0 \end{matrix}\right.[/m]

[m]\left\{\begin{matrix}
sinx=0\\cosx ≠ 0 \end{matrix}\right.[/m] или [m]\left\{\begin{matrix}
(2\sqrt{2}\cdot cosx -1)(2\sqrt{2}\cdot cosx +1)=0\\cosx ≠ 0 \end{matrix}\right.[/m]

[m]\left\{\begin{matrix}
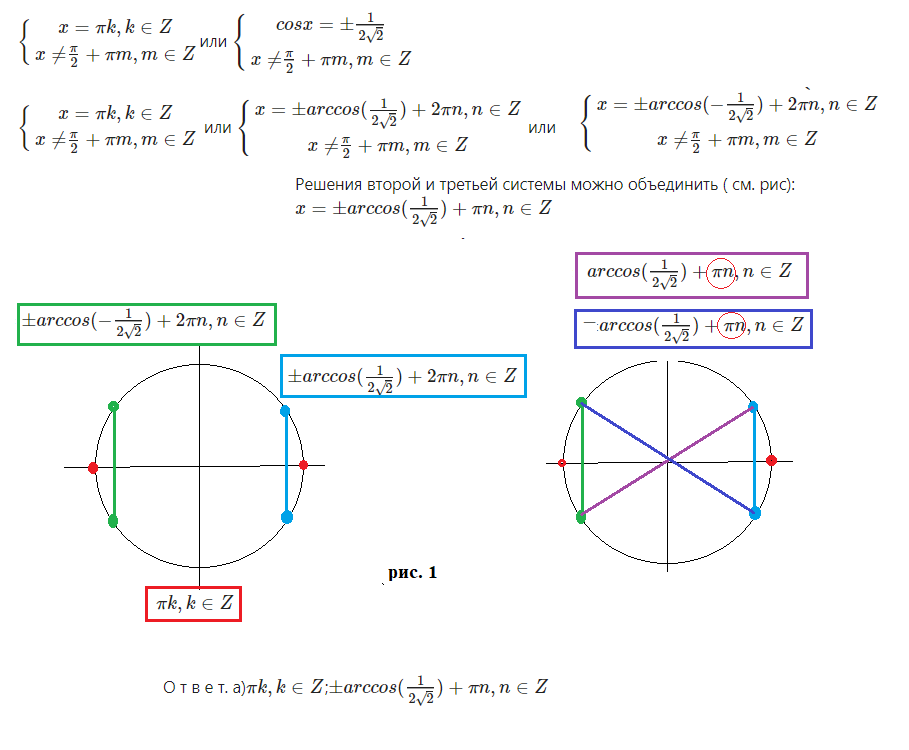
x=π k, k ∈ Z \\x ≠ \frac{π}{2}+πm, m ∈Z \end{matrix}\right.[/m]или [m]\left\{\begin{matrix}
cosx = ± \frac{1}{2\sqrt{2}}\\x ≠ \frac{π}{2}+πm, m ∈Z\end{matrix}\right.[/m]