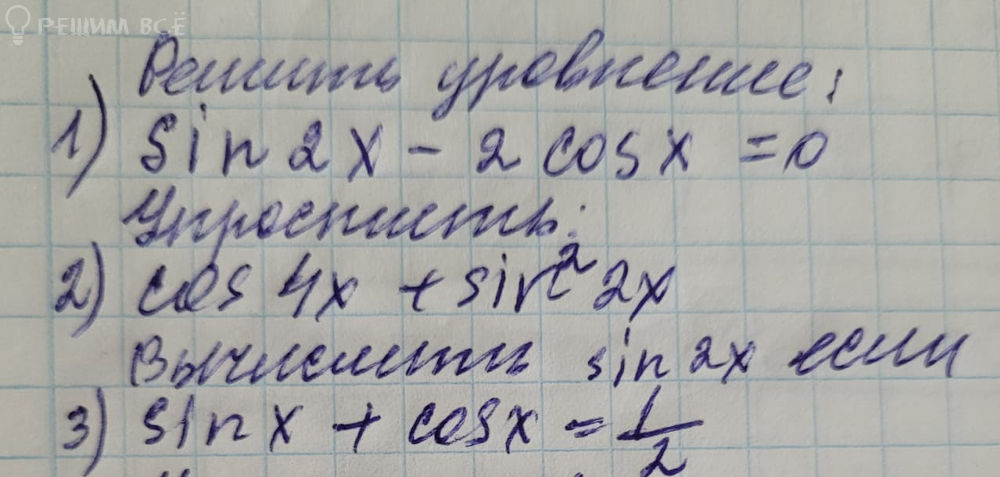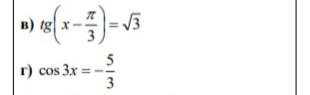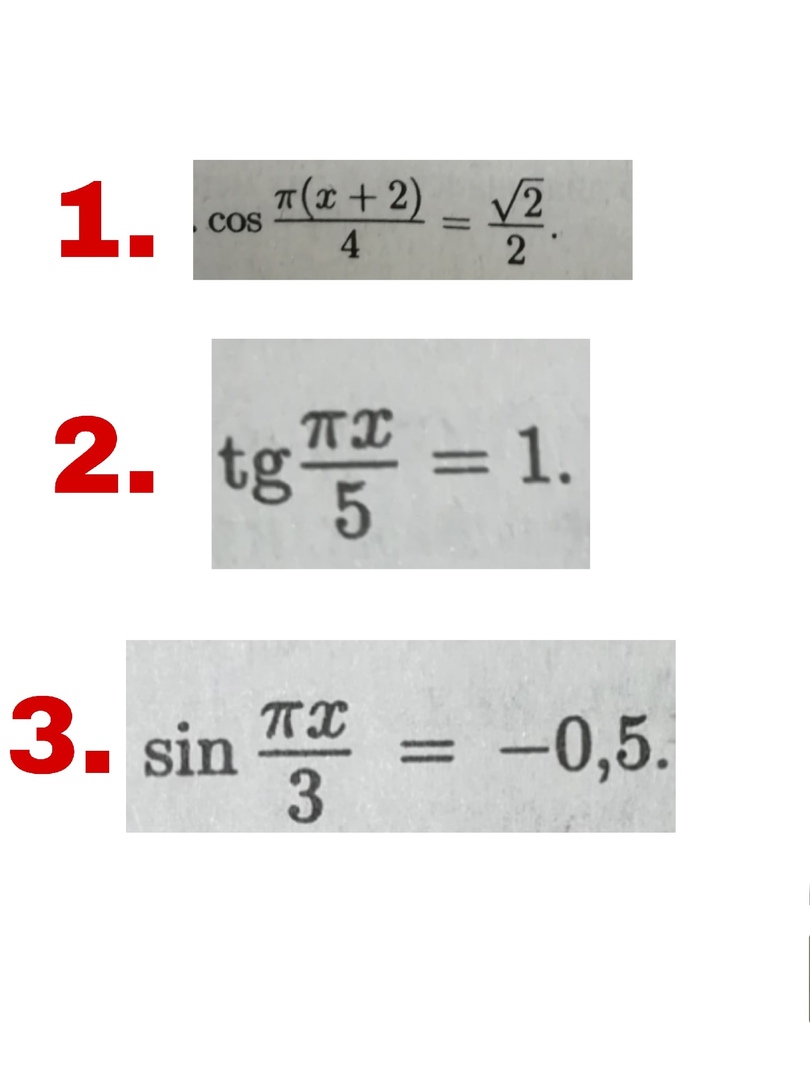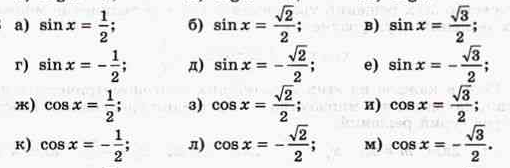Практика (17)
Отберите корни cosx = 0, [5Pi/2; 4Pi]

а) Решить уравнение:
5^2sin2x = (1/25)^cos(3π/2 + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π/2 ; 3π]
Поможіть пж дуже сильно нада cos4x-cos2x+sin3x=0
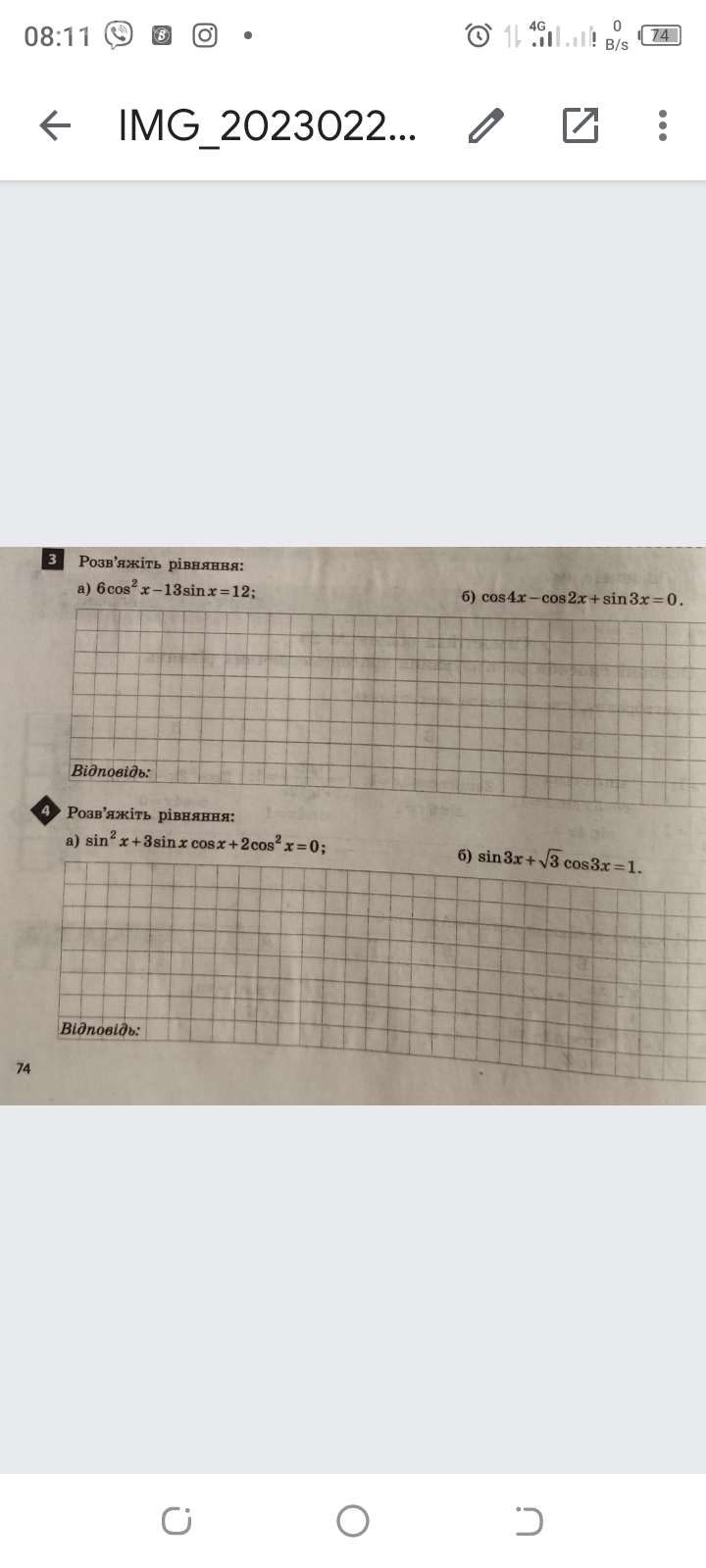
Нужна ваша помощь, если поможете буду благодарен ))
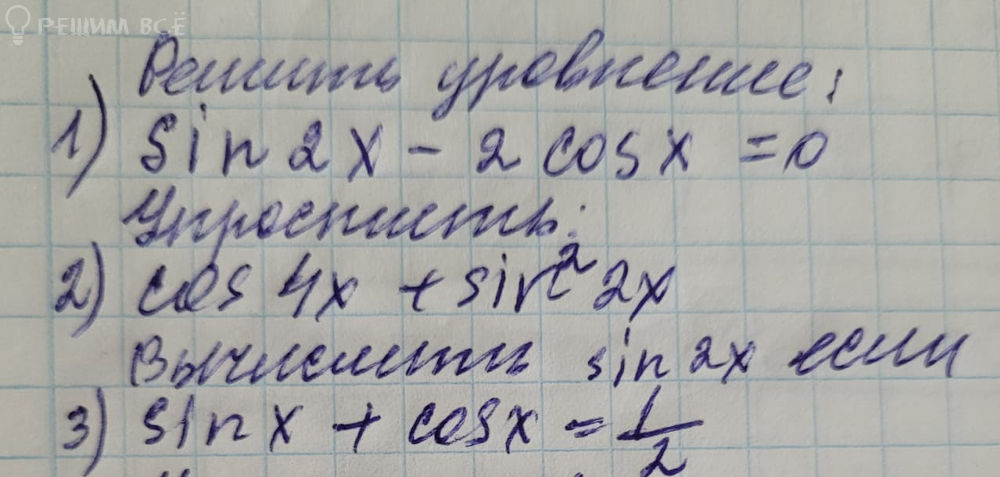
Решите уравнение: (4cos^2x-1)sqrt(tgx)=0.Найдите корни этого уравнения, принадлежащие интервалу(0;2п)

решить 5 6 упражнение & > 3 `=< ^ £ A Ё g = О > 5 — ' — w Ё Ё ® & щ © Е . Е < 3 2 0 ее В Е ва = < ЭЕ .54 @ R Е 5 g s 2 g = па w5 8 3 = ® g8 B E Il Я 5 е ъ РЕ 8е §° ПНО ЕВ o = o St оо нЫ o ens :Ё o T T 0 * Ё o 5 ‚0 S0 S I - S 0 = ol ® ® ы ь © g S o © ~ o & © = <5 Т ST S & < = = оо o = < s | I ох о A i 3 T оо 5 Н o = = o = I = B 3 9w э& $ х & СОЁ g = В I g е I 8 ! & » 8 Ё Е | A ) & н]Ё'Ё g N < ol 5 B 8 || оя е "Э + = Е @ = = ЕН = . o It = - = 2 g 3 I = 5 ее 3 8 @ g L 3 (= o 9 & кЕ © т а @ 8 = = 5 ® Ё & 2 S o Ь е — Ё 2 & | s 8 ® — Е = = & - Е g Е s | 8 8 g g e g — X эа = = 8 T = e Е 2 g ` оее g 7 ‚ g © = '3 5‹ Ё ' оо g g == > =) LT | MV}% | ) o | e L]

sin(Pi/10 - x/2) = sqrt(2)/2
1. sin(3x/2) = sqrt(2)/2
2. tg(2x-Pi/3) = -5
Практическая работа № 26(п)
Тема: «Тригонометрические уравнения»
Вариант № 2
Решить уравнения:
1. 2cosx + √3 = 0
2. sin3x = √3/2
3. cos(x/2) = √3/2
4. ctg(x - π/4) = 1
5. 2sinxcosx - √2sinx = 0
6. 2sin²x - √3sinx = 0
помогите решить задание в) и г) подробное решение
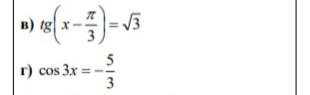
помогите решить а и б подробно

1. Решите уравнение: а) sinx=-1; б) cosx=√2/2; в) tgx=-√3.
2. а) cos²x-cos x-2=0; б) 3cos²x-2sinx+2=0.
3. а) sinx+ cosx=0; б) 3sin²x-2 √3 sinx cosx +cos²x=0.
4. а) cos x =- 0,5; б) sin x=1/4; в) tg x=2
5. а) sinx- cosx=1; б) 2cos²x-sin4x=1.
Найти корни уравнений. Спасибо за помощь заранее.
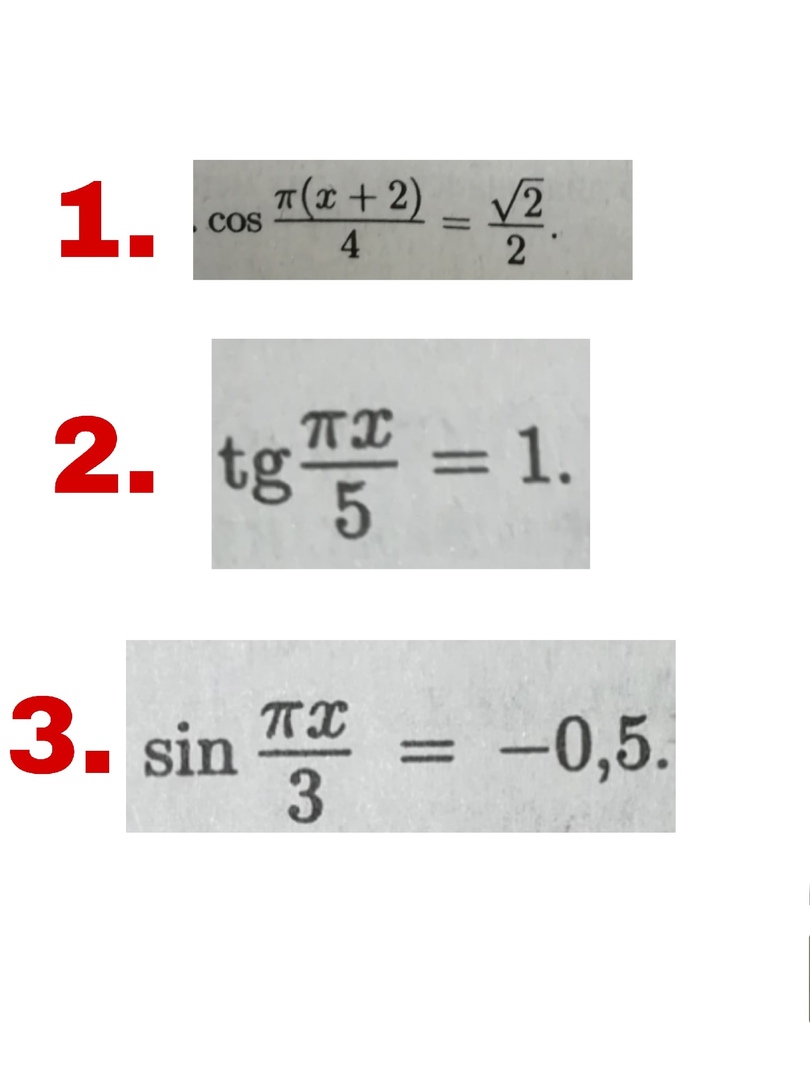
Алгебраическим решением, но если есть возможность, то и графическим, пожалуйста.
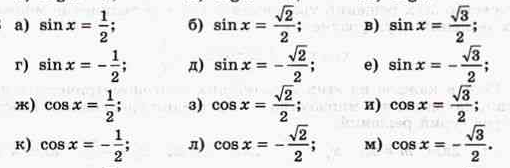
Решение задач
а) cos 2x = 1
б) cos 3x = -1
в) sin x/2 = -1
z) cos x/4 = 0
g) sin 2x/3 = 1
e) sin 5x = 0
решить тригонометрическое уравнение tgx равно минус 1 деленный на корень из трех (с рисунком окружности)
(решить под цифрой 3)