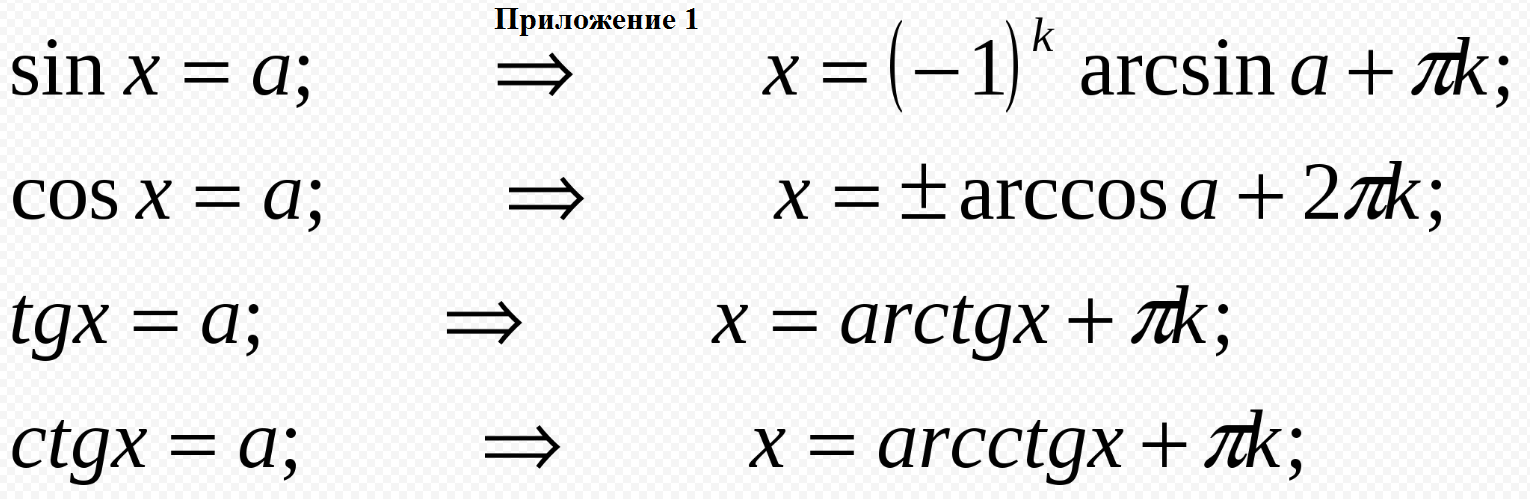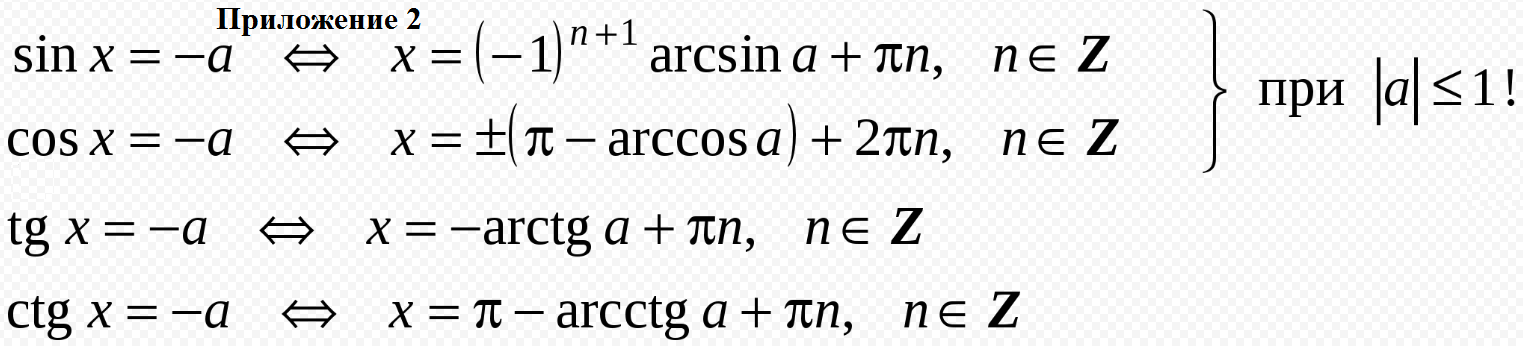Задача 45477 Помогите ,пожалуйста решить ....
Условие
Решение
1.
[i]Простейшие тригонометрические уравнения[/i].
Решают по формулам.
Cм. приложения 1 и 2:
a)[m]x=-\frac{\pi}{2}+2\pi n, n \in Z[/m]
( это [b]частный случай[/b] формулы для синуса)
б)[m]x=\pm arccos\frac{\sqrt{2}}{2}+2\pi k, k \in Z[/m] ⇒ [m]x=\pm \frac{\pi}{4}+2\pi k, k \in Z[/m]
в) [m]x=arctg(-\sqrt{3})+\pi n=-\frac{\pi}{3}+\pi n, n \in Z[/m]
2.
Квадратные уравнения или уравнения сводящиеся к квадратным.
[i]Замена переменной[/i]:
a)[red]cosx=t[/red]
t^2-t-2=0 ⇒ t=-1 или t=2
Получаем
cosx=-1 - простейшее как в п.1
cosx=2 не имеет решений, |cosx| ≤ 2
б)
сos^2x=1-sin^2x
[i]Замена переменной[/i]: [red]sinx=t[/red]
3.
[i]Однородные тригонометрические уравнения.[/i]
Делим
a) первое уравнение на cosx ≠ 0
б)второе уравнение cos^2x ≠ 0
Получаем
а) [i]простейшее уравнение [/i]относительно tgx
tgx=-1
[m]x=arctg(-1)+\pi n=-\frac{\pi}{4}+\pi n, n \in Z[/m]
б) квадратное уравнение относительно tgx
[m]3tg^2x-2\sqrt{3}tgx+1=0[/m]
[m](\sqrt{3}tgx-1)^2=0[/m]
[m]\sqrt{3}tgx-1=0[/m]
[m]tgx=\frac{1}{\sqrt{3}}[/m]
[m]x=arctg(\frac{1}{\sqrt{3}})+\pi k=\frac{\pi}{6}+\pi k, k \in Z[/m]
4.
[i]Простейшие тригонометрические уравнения[/i].
Решают по формулам.
Cм. приложения 1 и 2:
a)[m]x=\pm arccos(-0,5)+2\pi n, n \in Z[/m] ⇒
[m]x=\pm (\pi - arccos 0,5)+2\pi n=\pm (\pi - \frac{\pi}{3})+2\pi n=\pm\frac{2\pi}{3}+2\pi n, n \in Z[/m]
б)
[m]=(-1)^{k}\cdot arcsin\frac{1}{4}+\pi k, k \in Z[/m]
в) [m]x=arctg2+\pi k, k \in Z[/m]
5.
a) Решаем [i]методом введения вспомогательного угла[/i]
Делим уравнение на [m]\sqrt{2}[/m]
[m]\frac{1}{\sqrt{2}}sinx-\frac{1}{\sqrt{2}}cosx=\frac{1}{\sqrt{2}}[/m]
Вспомогательный угол φ :
sin φ =[m]\frac{1}{\sqrt{2}}[/m]
cos φ =[m]\frac{1}{\sqrt{2}}[/m]
φ =[m]\frac{\pi}{4}[/m]
Уравнение принимает вид:
[m]sin \frac{\pi}{4}sinx-cos\frac{\pi}{4}cosx=\frac{1}{\sqrt{2}}[/m]
Cлева формула:
[r]cos α cos β -sin α sin β =cos( α + β )[/r]
[m]-cos(x+\frac{\pi}{4})=\frac{1}{\sqrt{2}}[/m]
[m]cos(x+\frac{\pi}{4})=-\frac{1}{\sqrt{2}}[/m]
Простейшее уравнение, см. [i]приложение 2[/i]
[m]x+\frac{\pi}{4}=\pm arccos(-\frac{1}{\sqrt{2}})+2\pi n, n \in Z[/m]
[m]x+\frac{\pi}{4}=\pm (\pi - arccos\frac{1}{\sqrt{2}})+2\pi n, n \in Z[/m]
[m]x=\pm(\pi -\frac{\pi}{4})-\frac{\pi}{4}+2\pi n, n \in Z[/m]
[m]x=\pm(\frac{3 \pi}{4})-\frac{\pi}{4}+2\pi n, n \in Z[/m]
Запишем как две серии ответов:
[m]x=\frac{3 \pi}{4}-\frac{\pi}{4}+2\pi n, n \in Z[/m]
или
[m]x=-(\frac{3 \pi}{4})-\frac{\pi}{4}+2\pi n, n \in Z[/m]
О т в е т. [m]x=\frac{ \pi}{2}+2\pi n, n \in Z[/m]
или
[m]x=-\pi +2\pi n, n \in Z[/m]
5
б)
Применяем формулу:
[r]2 cos^2 α =1+cos2 α [/r]
Уравнение принимает вид:
cos2x-sin4x=0
Применяем формулу:
[r]sin2 α =2sin α cos α [/r]
cos2x-2sin2x*cos2x=0
cos2x*(1-2sin2x)=0
Простейшие уравнения:
сos2x=0 или 1-sin2x=0
[m]2x=\pm \frac{\pi}{2}+\pi k, k \in Z[/m] ( это тоже [i]частный[/i] случай)
[m]x=\pm \frac{\pi}{4}+\frac{\pi}{2} k, k \in Z[/m]
или
[m]sinx= \frac{1}{2}[/m]
[m]x=(-1)^{k}arcsin \frac{1}{2}+ \pi k, k \in Z[/m]
[m]x=(-1)^{k} \frac{\pi}{6}+ \pi k, k \in Z[/m]
О т в е т. [m]x=\pm \frac{\pi}{4}+\frac{\pi}{2} k, k \in Z[/m];[m]x=(-1)^{k} \frac{\pi}{6}+ \pi k, k \in Z[/m]
