Квадратные триг уравнения

5cos2x - 3cosx + 1
------------------------- = 0.
25sin^2x - 9

[7π/2 ; 5π]

а) Решите тригонометрическое уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку [-3п; -3п/2].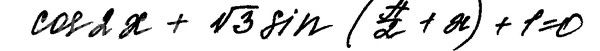

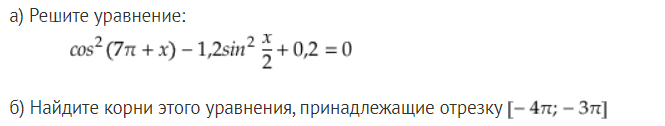
решите уравнение cos^2(7п+x)-1.2sin^2(x/2)+0.2=0. Найдите корни принадлежащие отрезку [-4п;-3п]

a) Решить -cos^2 x/2+sin^2 x/2=cos (-7pi+2x) . b) найти корни при при x от [-7pi;-4pi]

5) Найти наибольший отрицательный корень уравнения
sin^2x+cosx+1=0.

7) Найти все решения уравнения 2cos^2x = sinx, удовлетворяющие неравенству Pi/2 < x < Pi

9) Найти решения уравнения tg(2x-Pi/8) = sqrt(3) на промежутке (-3Pi; -5Pi/2)

10) Сколько корней имеет уравнение 2tgx+3ctgx=5 на промежутке [0°;360°]?

1. 7sin^2x+5sinx-2 = 0

2. 5sin^2x-21cosx-9 = 0

3. 5tgx-6ctgx+7 = 0

4. 4cosx+sinx = 0

Sin2 x + 5sin x - 6= 0

20.4. Решите однородное тригонометрическое уравнение:
1) 4cos^2x + sinxcosx + 3sin^2x - 3 = 0;


20.6. Найдите значение суммы корней уравнения:

2) 5cos^2x - 5cosx = 1 - 3sin^2x, если x ∈ [270; 450];