Задача 45913 Алгебраическим решением, но если есть...
Условие
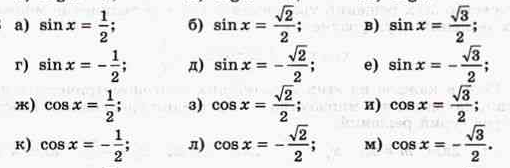
Решение
Они решаются по формулам.
[r]sinx=a
x=(-1)^(k)arcsina+πk, k ∈ Z[/r]
a)
[m]x=(-1)^{k}arcsin\frac{1}{2}+\pi k, k ∈ Z[/m]
[m]arcsin\frac{1}{2}=\frac {\pi}{6}[/m], так как [m] sin\frac {\pi}{6}=\frac{1}{2}[/m] и [m]\frac {\pi}{6}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
[m]x=(-1)^{k}\frac{\pi}{6}+\pi k, k ∈ Z[/m]
при k=2n
получаем
[m]x=\frac{\pi}{6}+ 2\pi n, n ∈ Z[/m]
при k=2n+1
получаем
[m]x=-\frac{\pi}{6}+ \pi +2\pi n=\frac{5\pi}{6}+2\pi n, n ∈ Z[/m]
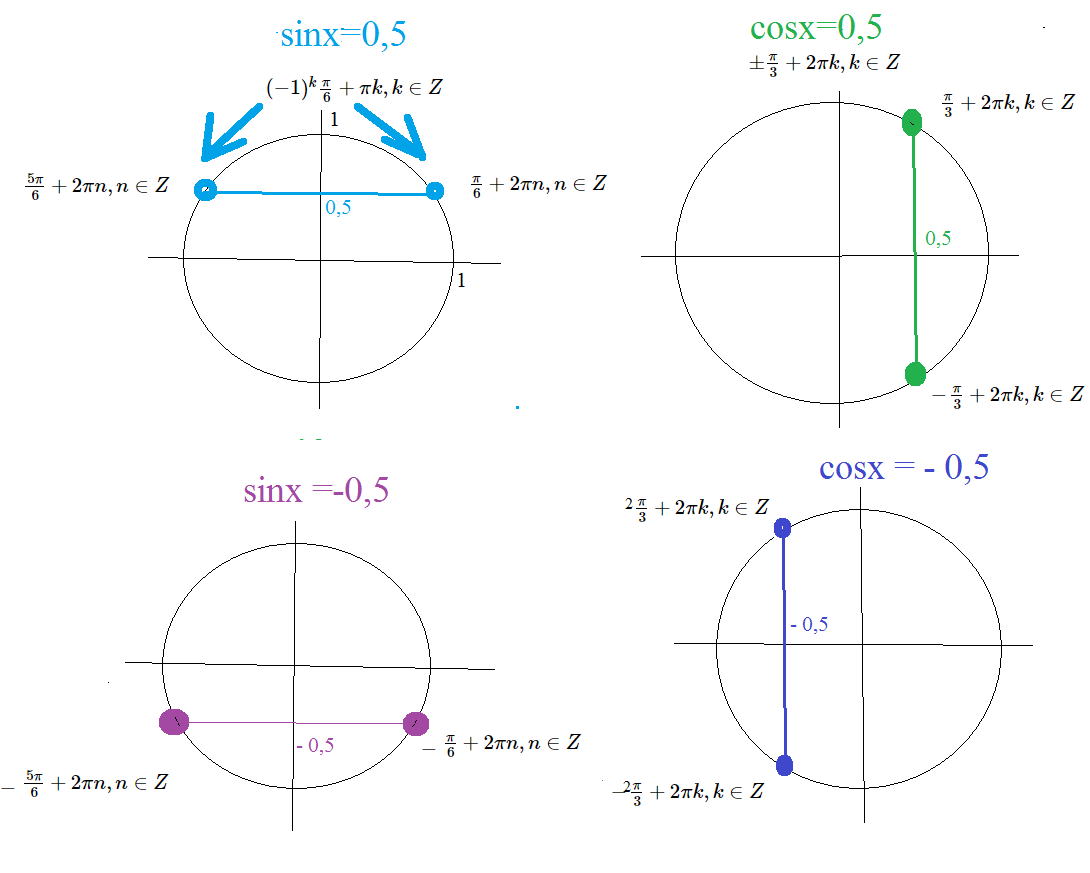
На рисунке ( см. рис.1):
г)
[m]x=(-1)^{k}arcsin (-\frac{1}{2})+\pi k, k ∈ Z[/m]
[m]x=(-1)^{k}(-\frac{\pi}{6})+\pi k, k ∈ Z[/m]
[m]x=-\frac{\pi}{6}+ 2\pi n, n ∈ Z[/m] или [m]x=-\frac{5\pi}{6}+2\pi n, n ∈ Z[/m]
ж)
[r]cosx=a
x= ± arccos a+2*πk, k ∈ Z[/r]
[m]x=\pm arccos\frac{1}{2}+2 \pi k, k ∈ Z[/m]
[m]arccos \frac{1}{2}=\frac {\pi}{3}[/m], так как [m] cos\frac {\pi}{3}=\frac{1}{2}[/m] и [m]\frac {\pi}{3}\in [0;\pi ][/m]
[m]x=\pm \frac{\pi}{3}+ 2\pi k, k ∈ Z[/m]
На рисунке ( см. рис.2)
к)
[m]x=\pm arccos(-\frac{1}{2})+2 \pi k, k ∈ Z[/m]
[m]arccos(- \frac{1}{2})=\pi - arccos\frac{1}{2}=\pi - \frac {\pi}{3}=\frac {2\pi}{3}[/m],
так как [m] cos\frac {2\pi}{3}=-\frac{1}{2}[/m] и [m]\frac {2\pi}{3}\in [0;\pi ][/m]
(cм. приложение 2)
[m]x=\pm \frac{2\pi}{3}+ 2\pi k, k ∈ Z[/m]