Задача 52953 sinx+cosx = 2sqrt(2)sinx*cosx ...
Условие
Решение

Все решения
sinx+cosx=t
Возводим в квадрат:
sin^2x+2sinx*cosx+cos^2x=t^2 ⇒ так как sin^2x+cos^2x=1, то
2sinx*cosx=t^2-1
Получаем уравнение:
t=sqrt(2)*(t^2-1)
sqrt(2)t^2-t-sqrt(2)=0
D=1+8=9
t_(1)=[m]-\frac{1}{\sqrt{2}}[/m] [blue]или[/blue] t_(1)=[m]\sqrt{2}[/m]
Обратный переход:
sinx+cosx= [m]-\frac{1}{\sqrt{2}}[/m] [blue]или[/blue] sinx+cosx= [m]\sqrt{2}[/m]
Так как sinx=cos([m]\frac{\pi}{2}[/m]-x), то
cos([m]\frac{\pi}{2}[/m]-x)+cosx= [m]-\frac{1}{\sqrt{2}}[/m] или cos([m]\frac{\pi}{2}[/m]-x)+cosx= [m]\sqrt{2}[/m]
Применяем формулу [r]cos α +cos β =2cos(( α + β )/2) * cos(( α - β )/2)[/r]
2cos[m]\frac{\pi}{4}[/m]*cos([m]\frac{\pi}{4}[/m]-x)=[m]-\frac{1}{\sqrt{2}}[/m] [blue]или[/blue] 2cos[m]\frac{\pi}{4}[/m]*cos([m]\frac{\pi}{4}[/m]-x)=[m]\sqrt{2}[/m]
Так как cos[m]\frac{\pi}{4}[/m]=[m]\frac{\sqrt{2}}{2}[/m]
[m]\sqrt{2}[/m]*cos([m]\frac{\pi}{4}[/m]-x)=[m]-\frac{1}{\sqrt{2}}[/m] [blue]или[/blue] [m]\sqrt{2}[/m]*cos([m]\frac{\pi}{4}[/m]-x)=[m]\sqrt{2}[/m]
cos([m]\frac{\pi}{4}[/m]-x)=[m]-\frac{1}{2}[/m] [blue]или[/blue] cos([m]\frac{\pi}{4}[/m]-x)=[m]1[/m]
По свойству четности косинуса
cos([m]\frac{\pi}{4}[/m]-x)=cos(x-[m]\frac{\pi}{4}[/m])
cos(x-[m]\frac{\pi}{4}[/m])=[m]-\frac{1}{2}[/m] [blue]или[/blue] cos(x-[m]\frac{\pi}{4}[/m])=[m]1[/m]
x-[m]\frac{\pi}{4}=\pm\frac{2\pi}{3}+2\pi[/m] n,n ∈ Z [blue]или[/blue] x-[m]\frac{\pi}{4}=2\pi[/m] m,m ∈ Z
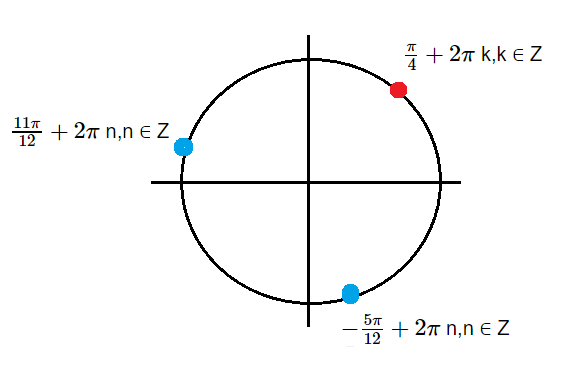
x=[m]\frac{\pi}{4}+\frac{2\pi}{3}+2\pi[/m] n,n ∈ Z ⇒ x=[m]\frac{11\pi}{12}+2\pi[/m] n,n ∈ Z ⇒
x=[m]\frac{\pi}{4}-\frac{2\pi}{3}+2\pi[/m] n,n ∈ Z ⇒x=[m]-\frac{5\pi}{12}+2\pi[/m] n,n ∈ Z
x=[m]\frac{\pi}{4}+2\pi[/m] m,m ∈ Z
О т в е т.
[m]\frac{11\pi}{12}+2\pi[/m] n,n ∈ Z ⇒
[m]-\frac{5\pi}{12}+2\pi[/m] n,n ∈ Z
[m]\frac{\pi}{4}+2\pi[/m] m,m ∈ Z
см. рис.
То, что эти три ответа можно объединить в один: [m]\frac{\pi}{4}+\frac{2\pi}{3}[/m]k, k ∈ Z
- это [red]проблема взрослых[/red]
Задача решена верно и если ответ не засчитан
можно смело идти на апелляцию