Задача 32665 sin(п+x)*sin(2x-3п/2) = 1...
Условие
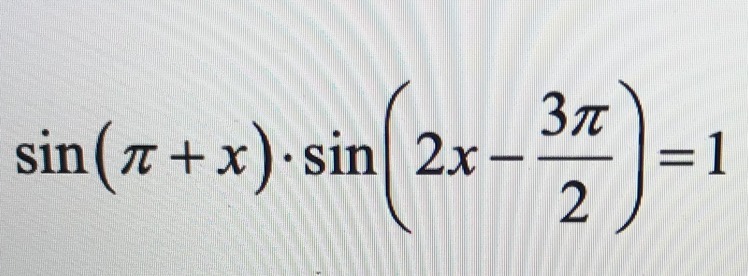
Решение
По формулам приведения sin(pi+x)=-sinx, sin(2x-3pi/2)=cos2x,
Получаем уравнение -sinx*cos2x=1. cos2x=1-2sin^2(x), поэтому
-sinx*(1-2sin^2(x))-1=0 Решим уравнение 2sin^3(x)-sinx-1=0,
Разложим на множители заменив -sinx на выражение -2x+x . получим 2sin^3(x)-2sinx+sinx-1=0, 2sinx(sin^2(x)-1)+(sinx-1)=0,
или (sinx-1)*(2sin^2(x)+2sinx+1)=0
sinx=1, отсюда x=pi/2+2pik,k- целое число.
2sin^2(x)+2sinx+1=0 решений не имеет так как D<o
Ответ: x=pi/2+2pik.k-целое число.
Все решения
1) каждый множитель равен 1
{sin(π+x)=1 ⇒ -sinx=1 ⇒ sinx=-1;
{sin(2x-(3π/2))=1 ⇒ -sin((3π/2)-2x)=1 ⇒ cos2x=1
{sinx=-1 ⇒ х=(-π/2)+2πn, n∈ Z
{cos2x=1 ⇒ 2x=2πk, k∈ Z; x=2πk, k∈ Z
Cистема не имеет решений
2) каждый множитель равен -1
{sin(π+x)=-1 ⇒ -sinx=-1 ⇒ sinx=1;
{sin(2x-(3π/2))=-1 ⇒ -sin((3π/2)-2x)=-1 ⇒ cos2x=-1
{sinx=1 ⇒ х=(π/2)+2πn, n∈ Z
{cos2x=-1 ⇒ 2x=π + 2πk, k∈ Z; x=(π/2)+ πk, k∈ Z
общее решение двух уравнений
(π/2)+2πn, n∈ Z
О т в е т. (π/2)+2πn, n∈ Z
