Задача 63382 ...

61d9de1eacffe413ad532e0b

26.02.2022 17:26:27

а) решите уравнение 2cos^(3)x +3cos^(2)x+cosx/sqrt(ctgx)=0
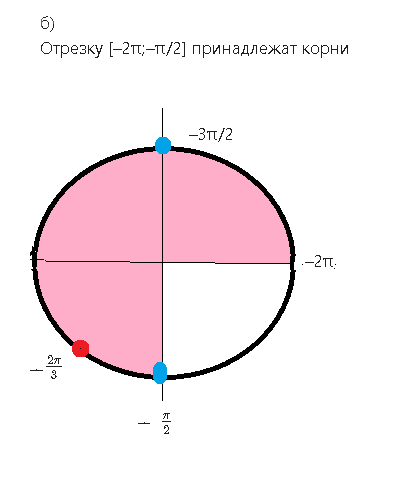
б)найдите все корни этого уравнения принадлежащие промежутку [-2π;-π/2]

5f3ea7e3faf909182968ddd9

27.02.2022 00:01:08

★

ОДЗ: ctgx >0

2cos3x +3cos2x+cosx/√ctgx=0

Дробь равна 0 когда числитель равен 0, а знаменатель отличен от нуля.

[m]\left\{\begin {matrix}2cos^3x +3cos^2x+cosx=0\\ctgx ≠ 0\end {matrix}\right.[/m]


[m]2cos^3x +3cos^2x+cosx=0[/m]

[m]cosx*(2cos^2x+3cosx+1)=0[/m] ⇒ D=9-4*2*1=1; корни (-3 ± 1)/4


[m]cosx=0[/m] или [m]cosx=-1[/m] или [m]cosx=-1/2[/m]


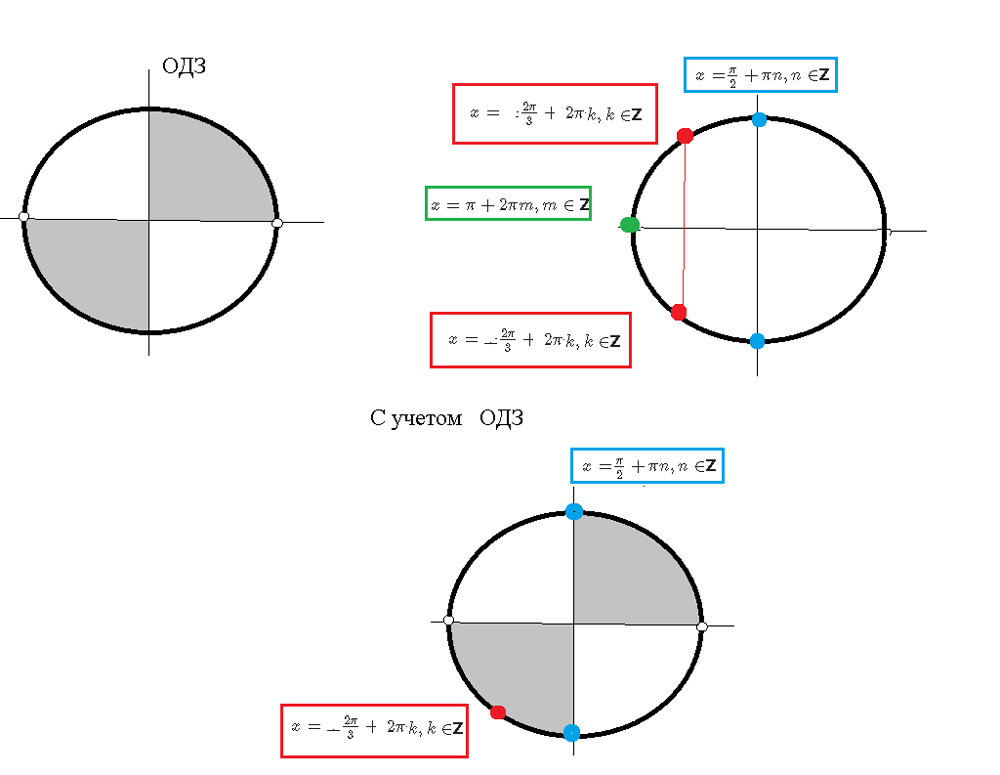
[m]x=\frac{π}{2}+πn, n ∈ [/m][b]Z[/b] или [m]x=π+2πm, m ∈ [/m] [b]Z [/b] или [m]x= ±\frac{2π}{3}+2πk, k ∈ [/m][b]Z[/b]


C учетом ОДЗ получаем ответ
[m]\frac{π}{2}+πn, n ∈ [/m][b]Z[/b]; [m] ±\frac{2π}{3}+2πk, k ∈ [/m][b]Z[/b]