Задача 63381 ...
Условие
б) укажите корни этого уровнения принадлежащие отрезку [-2π;-π/2]
математика 10-11 класс
482
Решение
★
tg(π-x)=-tgx
cos(3π/2–2x)=-sin2x
Так как
sin 5π/6=1/2
уравнение принимает вид:
-tgx*(-sin2x)=1/2
По формулам:
tgx=sinx/cosx
sin2x=2sinx*cosx
уравнение принимает вид:
-(sinx/cosx)*(-2sinx*cosx)=1/2
sin^2x=1/4
cosx ≠ 0
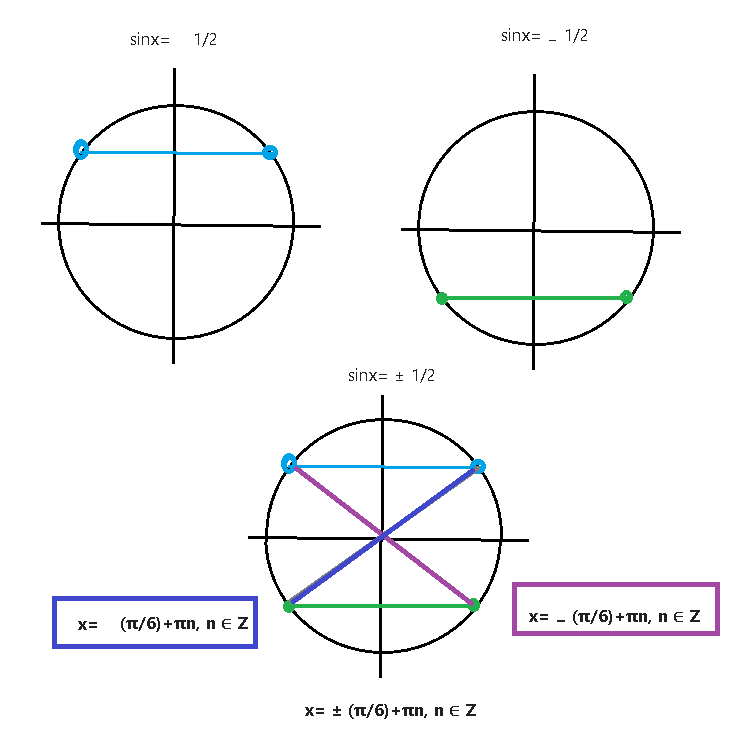
sin^2x=1/4 ⇒ sinx= ± 1/2
[b]x= ± (π/6)+πn, n ∈ Z[/b]
а)О т в е т. [b]x= ± (π/6)+πn, n ∈ Z[/b]
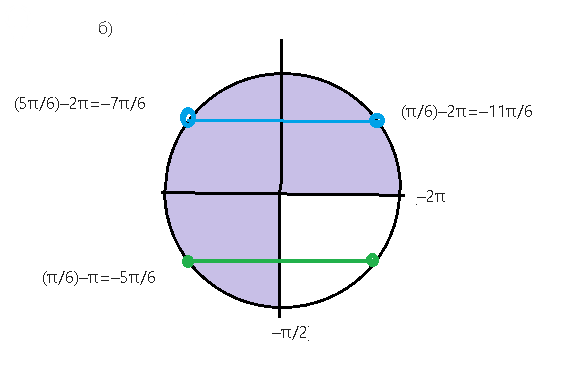
б)
отрезку [–2π;–π/2] принадлежат корни:
(π/6)-2π=-11π/6
(5π/6)-2π=-7π/6
(π/6)-π=-5π/6