Задача 45346 Помогите решить адание д) и е)...
Условие
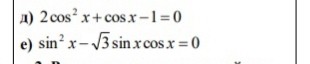
математика
672
Решение
★
[i]Замена переменной[/i]:
cosx=t
2t^2+t-1=0
D=1-4*2*(-1)=9
t=(-1 ± 3)/4
t=-1 или t=1/2
Обратный переход:
cosx=-1 ⇒ x=π+2πn, n ∈ Z
cosx=1/2 ⇒ x= ± arccos(1/2)+2πm, m ∈ Z ⇒ x= ± (π/3)+2πm, m ∈ Z
О т в е т. π+2πn,± (π/3)+2πm, n, m ∈ Z
е)
sinx*(sinx-sqrt(3)cosx)=0
sinx=0 ⇒ x=πk, k ∈ Z или sinx-sqrt(3)cosx=0 ⇒ делим на сosx ≠ 0
tgx=sqrt(3) ⇒
x=(π/3)+πn, n ∈ Z
О т в е т. πk, (π/3)+πn, k, n ∈ Z
