Задача 49007 Срочно нужна помощь. Математика профиль...

tunnerr

2020-04-30 12:32:24

Срочно нужна помощь. Математика профиль 13 задание

sova

2020-04-30 12:52:15

а)
Решаем [i]по определению логарифма[/i]

3^(2x)-sqrt(2)sinx-sin2x=9^(x)

Так как 9^(x) > 0 при любом х, выражение под знаком логарифма положительно, и потому нет ОДЗ

Так как 9^(x)=3^(2x)

уравнение принимает вид:

2*sinx*cosx+sqrt(2)sinx=0 (применили формулу синуса двойного угла)

Раскладываем левую часть на множители:

sinx* (2cosx+sqrt(2))=0

sinx=0 ⇒ x=πk, k ∈ Z

2cosx+sqrt(2)=0 ⇒ cosx=-sqrt(2)/2 ⇒ x= ± arccos(-sqrt(2)/2)+2πn, n ∈ Z

x= ± (π- arccos(sqrt(2)/2))+2πn, n ∈ Z;

x= ± (3π/4)+2πn, n ∈ Z;


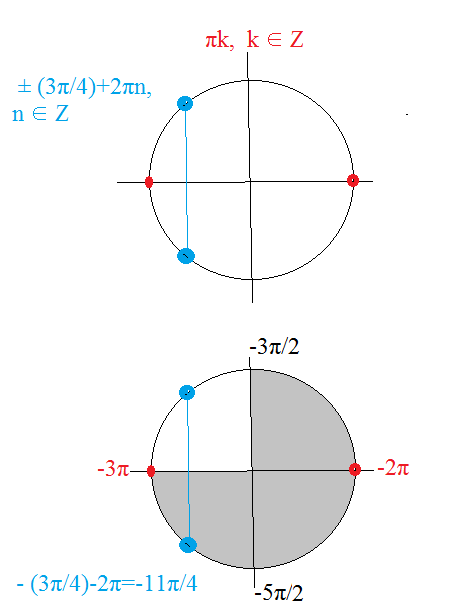
О т в е т. πk, ± (3π/4)+2πn, k, n ∈ Z ( см. рис.1)

б)
Указанному промежутку принадлежат три корня:
-3π; -2π;

- (3π/4)-2π=-11π/4

( см. рис. 2)