Задача 60520 ...
Условие
[block](4sin^4x+3cos2x-1)/(sqrt(tgx)) = 0[/block]
Найти все корни уравнения на отрезке [3π/2; 3π].
Решение
[m]tgx>0[/m] ⇒ [m] πk < x < \frac{π}{2}+πk, k ∈ [/m] [b]Z[/b] ⇒ углы в первой и третьей четвертях
Дробь равна нулю тогда и только тогда, когда числитель равен 0, а знаменатель отличен от нуля.
Отличие знаменателя от 0 учтено в ОДЗ.
[m]4sin^4x+3cos2x-1=0 [/m]
Так как
[m] cos2x=1-2sin^2x[/m], получим уравнение:
[m]4sin^4x+3(1-2sin^2x)-1=0 [/m]
Это [i]биквадратное[/i] уравнение относительно sinx
[m]4sin^4x+3(1-2sin^2x)-1=0 [/m]
[m]4sin^4x-6sin^2x+2=0 [/m]
[m]2sin^4x-3sin^2x+1=0 [/m]
D=(-3)^2-4*2=1
sin^2x=1/2 ИЛИ sin^2x=1
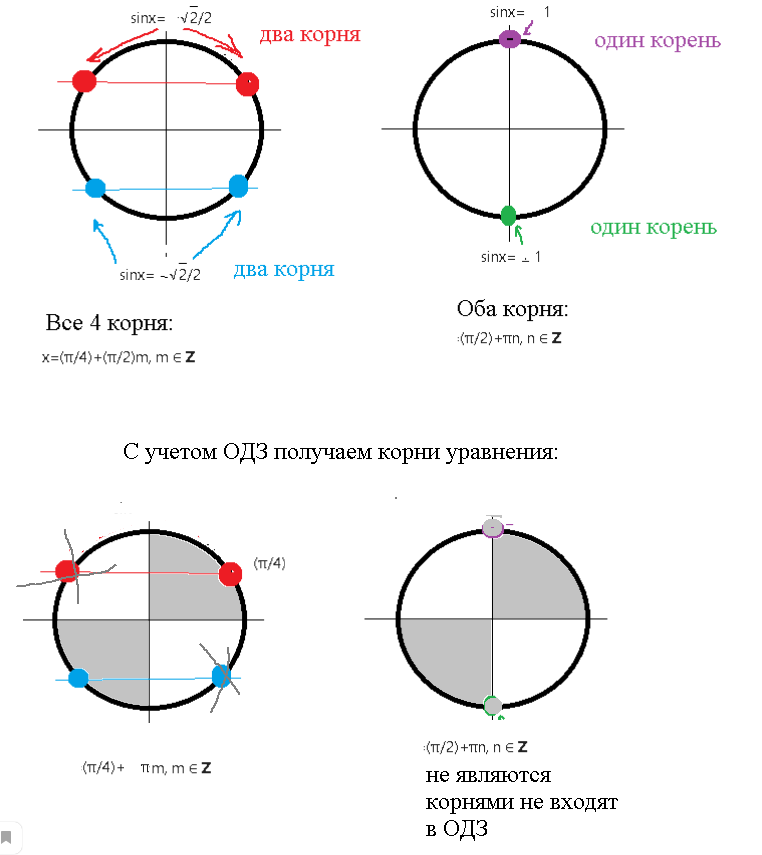
sin^2x=1/2 ⇒ sinx= ±sqrt(2)/2 ⇒ x=(π/4)+(π/2)m, m ∈ [b]Z[/b] Не все корни удовлетворяют ОДЗ
Только те, которые лежат в первой и третьей четвертях
ИЛИ
sin^2x=1 ⇒ sinx= ± 1 ⇒ [m] x=\frac{π}{2}+πn, n[/m] ∈ [b]Z[/b] найденные корни не удовлетворяют ОДЗ
[red]С учетом ОДЗ [/red] получаем ответ.
О т в е т.[m] \frac{π}{4}+πn, n ∈ [/m] [b]Z[/b]
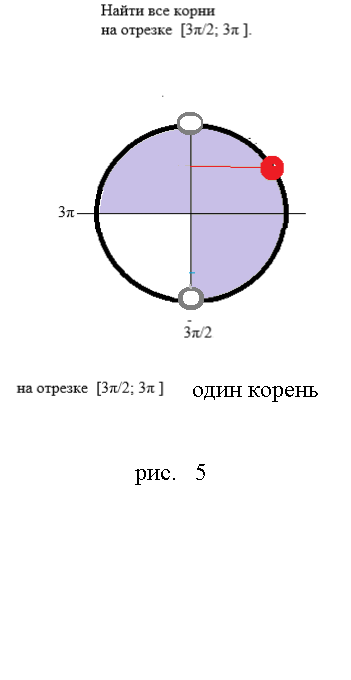
На отрезке [m][\frac{3π}{2};3π][/m] один корень ( см. рис. 5)
[m]\frac{π}{4}+2π=\frac{9π}{4} [/m];