Задача 61110 Решение этого примера sqrt(2tg(3Pi/2 -...
Условие
sqrt(2tg(3Pi/2 - x)sin(3Pi-2x)) = -tg(2Pi/3)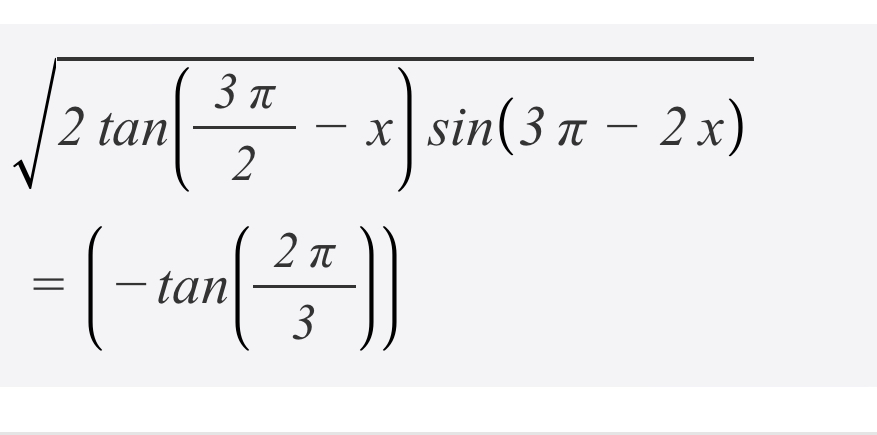
Решение
[m]tg(\frac{3π}{2}-x)=ctgx[/m]
[m]sin(3π-2x)=sin2x[/m]
[m]\sqrt{2\cdot ctgx \cdot sin2x }=\sqrt{2\cdot \frac{cosx}{sinx} \cdot 2sinx cosx}=2\sqrt {cos^2x}=2|cosx|[/m]
[m]-tg\frac{2π}{3}=-(tg(π-\frac{π}{3})=-(-tg\frac{π}{3})=tg\frac{π}{3}=\sqrt{3}[/m]
Уравнение принимает вид:
[m]2|cosx|=\sqrt{3}[/m] ⇒
[m]|cosx|=\frac{\sqrt{3}}{2}[/m] ⇒
[m]cosx=\frac{\sqrt{3}}{2}[/m] или [m]cosx=-\frac{\sqrt{3}}{2}[/m]
Простейшие тригонометрические уравнения:
[m]x= ± arccos\frac{\sqrt{3}}{2}+2πk, k ∈ [/m] [b]Z[/b] или [m]x= ± arccos(-\frac{\sqrt{3}}{2})+2πn, n ∈ [/m][b]Z[/b]
[m]x= ±\frac{π}{6}+2πk, k ∈ [/m] [b]Z[/b] или [m]x= ± (π-\frac{π}{6})+2πn, n ∈ [/m][b]Z[/b]
О т в е т. [m]x= ±\frac{π}{6}+2πk, k ∈ [/m] [b]Z[/b] или [m]x= ± \frac{5π}{6}+2πn, n ∈ [/m][b]Z[/b]