Задача 57578 а) Решите уравнение tg(Pi-x)cos(3Pi/2 -...

60119d6f5d2ce76e3c5678d0

31.01.2021 16:26:22

а) Решите уравнение tg(Pi-x)cos(3Pi/2 - 2x) = sin 5Pi/6

б) Укажите корни этого уравнения, принадлежащие отрезку [-2Pi; -Pi/2]

5f3ea7e3faf909182968ddd9

02.02.2021 00:09:44

★

По формулам приведения:

[m]tg(π-x)=-tgx[/m]

[m]cos(\frac{3π}{2}-2x)=-sin2x[/m]

Так как [m] sin\frac{5π}{6}=\frac{1}{2}[/m]

уравнение принимает вид:

[m](-tgx)\cdot (-sin2x)=\frac{1}{2}[/m]

⇒

[m]\frac{sinx}{cosx}\cdot 2 sinx\cdot cosx=\frac{1}{2}[/m]


[m]cosx ≠ 0 [/m]

[m]sin^2x=\frac{1}{4}[/m]



[m]sinx= ± \frac{1}{2}[/m]

[m]sinx= \frac{1}{2}[/m] или [m]sinx= \frac{1}{2}[/m]

[m]x=(-1)^{n+1}\frac{π}{6}+πn, n ∈ [/m] [b]Z[/b] или [m]x=(-1)^{m}\frac{π}{6}+πm, m ∈ [/m] [b]Z[/b]


Получаем две серии ответов, которые можно объединить:

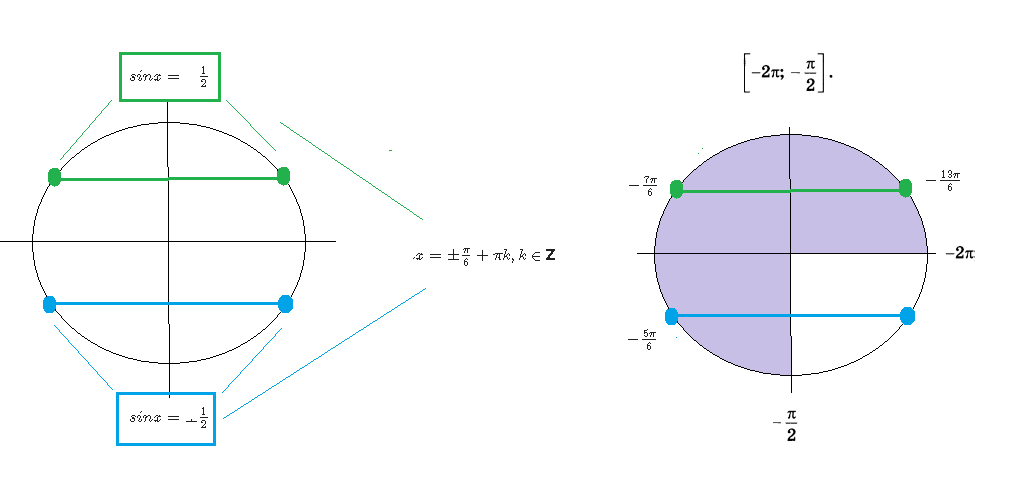
[m]x= ± \frac{π}{6}+πk, k ∈ [/m][b] Z[/b]

( см. рис.)


Указанному отрезку принадлежат корни:

[m]-\frac{13π}{6}; -\frac{7π}{6};-\frac{5π}{6}[/m]

( см. рис.)