Задача 43697 ...

vk229746389

2020-01-26 14:45:49

Решите тригонометрические уравнения

4.2.22.

8sin^4x+13cos2x = 7
270 < x < 360

4.2.28.

tgx-5tg(x-5Pi/2) = 6sin(13Pi/2)
Pi ≤ x ≤ Pi

sova

2020-01-26 20:12:38

★

tg(x-(5π/2))=-tg((5π/2)-x)=-tgx

sin(13π/2)=sin(6π+(π/2))=sin(π/2)=1

[b]tgx-5*(-tgx)=6[/b]

6tgx=6

tgx=1

x=(π/4)+πn, n ∈ Z

-π ≤ [b](π/4) [/b]≤ π


2.

cos2x=1-2sin^2x

Получаем биквадратное уравнение относительно sinx

8sin^4x-26sin^2x+6=0

4sin^4x-13sin^2x+3=0

D=(-13)^2-4*4*3=169-48=121

sin^2x=1/4; sin^2x=3

⇒ sinx= ± 1/2; sinx= ± sqrt(3)


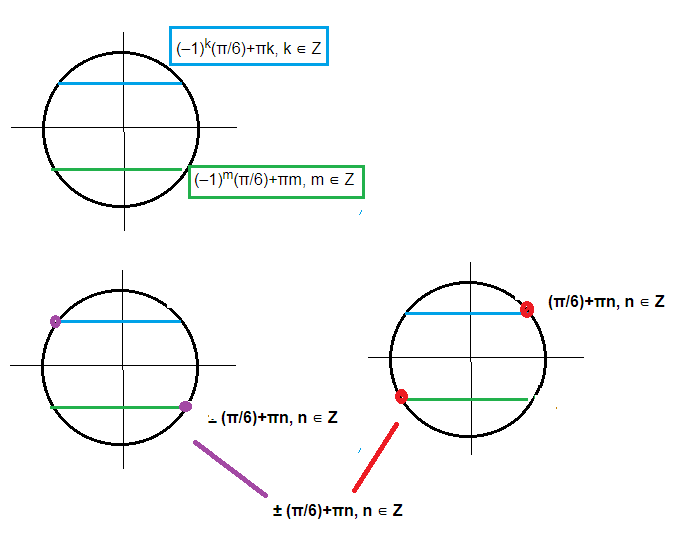
sinx= 1/2 ⇒ (-1)^(k)(π/6)+πk, k ∈ Z


sinx=-1/2⇒ (-1)^(m)(π/6)+πm, m ∈ Z

можно объединить и записать так:
[b] ± (π/6)+πn, n ∈ Z[/b]


sinx=sqrt(3) - уравнение не имеет корней

sinx=-sqrt(3) - уравнение не имеет корней


О т в е т. [b] ± (π/6)+πn, n ∈ Z[/b]