Задача 55125 а) Решите уравнение tg8x-tg3x=sin5x б)...
Условие
б) найдите все корни уравнения на отрезке [-п/2;п]
Решение
[m]\frac{sin8x}{cos8x}-\frac{sin3x}{cos3x}=sin5x[/m]
[m]\frac{sin8x\cdot cos3x-sin3x\cdot cos8x}{cos8x\cdot cos3x}=sin5x[/m]
Формула в числителе [r]sin α *cos β -cos α *sin β =sin( α - β )[/r]
[m]\frac{sin(8x-3x)}{cos8x\cdot cos3x}=sin5x[/m]
[m]\frac{sin5x}{cos8x\cdot cos3x}-sin5x=0[/m]
[m]sin5x\cdot (\frac{sin5x}{cos8x\cdot cos3x}-1)=0[/m]
[m]\left\{\begin{matrix}sin5x=0\\cos8x\cdot cos3x ≠0 \end{matrix}\right.[/m] или [m]\left\{\begin{matrix}\frac{sin5x}{cos8x\cdot cos3x}-1=0\\cos8x\cdot cos3x ≠0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}5x=πk, k ∈ Z\\8x ≠\frac{π}{2}+πn и 3x ≠ \frac{π}{2}+πm, n ∈Z, m ∈ Z \end{matrix}\right.[/m] или [m]\left\{\begin{matrix}sin5x=cos8x\cdot cos3x\\8x ≠\frac{π}{2}+πn и 3x ≠ \frac{π}{2}+πm, n ∈Z, m ∈ Z \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}x=\frac{π}{5}k, k ∈ Z\\x ≠\frac{π}{16}+\frac{π}{8}n и x ≠ \frac{π}{6}+\frac{π}{3}m, n ∈Z, m ∈ Z \end{matrix}\right.[/m] или [m]\left\{\begin{matrix}sin(8x-3x)=cos 8x\cdot cos3x\\x ≠\frac{π}{16}+\frac{π}{8}n и x ≠ \frac{π}{6}+\frac{π}{3}m, n ∈Z, m ∈ Z \end{matrix}\right.[/m]
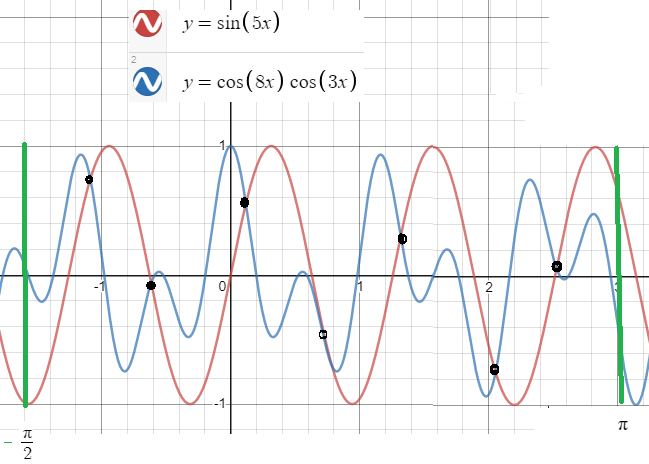
Решение второй системы графически на рис.
б)
Из первой серии ответов отрезку [-π/2; π] принадлежат корни:
[m]-\frac{2π}{5}[/m]; [m]-\frac{π}{5}[/m]; 0; [m]\frac{π}{5}[/m]; [m]\frac{2π}{5}[/m]; [m]\frac{3π}{5}[/m]; [m]\frac{4π}{5}[/m]
На рис корни второй системы есть, отрезку принадлежат еще 7 корней.
Вопрос. Где взят пример, укажите источник, если можно фото.