Задача 31326 3. 4cos(x/4 + Pi/6) = sqrt(3) 4....

bilikto555

2018-11-27 14:23:49

3. 4cos(x/4 + Pi/6) = sqrt(3)

4. [m]\frac{2sinx+\sqrt{3}}{2cosx+1} =0[/m]

sova

2018-11-27 14:56:38

★

3.
cos((x/4)+(π/6))=sqrt(3)/4
(x/4)+(π/6)= ± arccos(sqrt(3)/4)+2πn, n∈ Z
(x/4)= ± arccos(sqrt(3)/4) -(π/6) +2πn, n∈ Z
x= ±4*arccos(sqrt(3)/4) -4*(π/6) +8πn, n∈ Z
[b]x= ±4*arccos(sqrt(3)/4) -(2π/3) +8πn, n∈ Z[/b]

4.
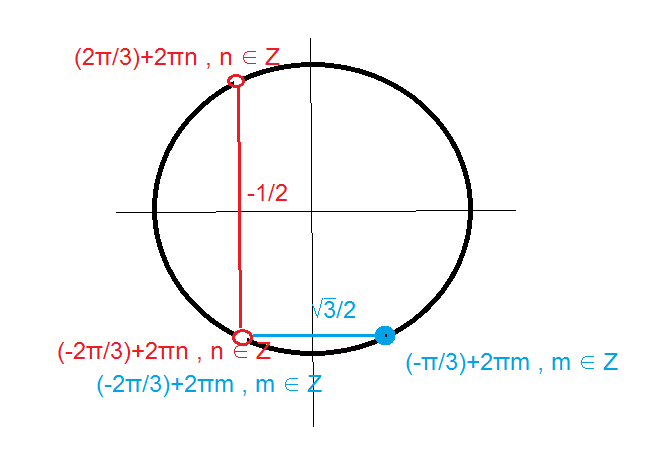
{2sinx+sqrt(3)=0 ⇒sinx=-sqrt(3/2)
{2cosx+1 ≠ 0 ⇒ cosx ≠ -1/2

{x=(-1)^(k)*arcsin((-sqrt(3))/2)+πk, k ∈ Z
{x ≠ ± arccos(-1/2)+2πn , n ∈ Z

{x=(-π/3)+2πm, m ∈ Z или x=(-2π/3)+2πm, m ∈ Z
{x ≠ (±2π/3)+2πn , n ∈ Z

О т в е т. [b](-π/3)+2πm, m ∈ Z[/b]