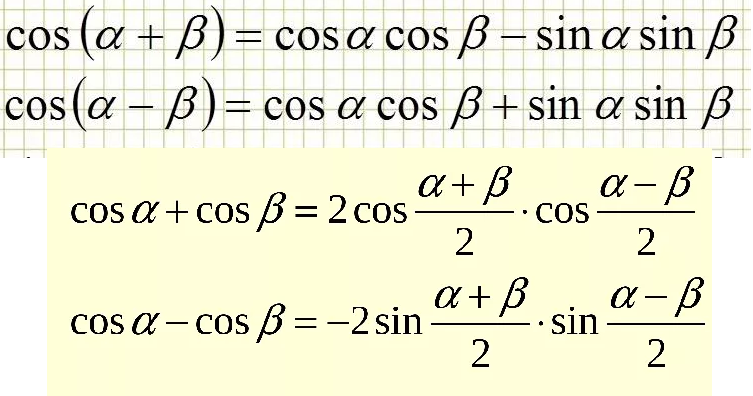Задача 43695 ...

vk229746389

26 января 2020 г. в 14:44

Решите тригонометрические уравнения

4.4.12
cos7x – sin 5x =√3(cos5x – sin7x)
0<x<30°

4.4.15
(sinx +√3 cosx)²–5 = cos(π/6 – x)

sova

26 января 2020 г. в 20:33

cos7x–√3sin7x=sin5x+√3cos5x

Делим обе части уравнения на 2:

[m]\frac{1}{2}cos7x-\frac{\sqrt{3}}{2}sin7x=\frac{1}{2}sin5x+\frac{\sqrt{3}}{2}cos5x[/m]

Заменим слева
[m]\frac{1}{2}=cos\frac{\pi}{3}[/m]

[m]\frac{\sqrt{3}}{2}=sin\frac{\pi}{3}[/m]

справа:

[m]\frac{1}{2}=sinx\frac{\pi}{6}[/m]

[m]\frac{\sqrt{3}}{2}=cos\frac{\pi}{6}[/m]

[m]cos\frac{\pi}{3}\cdot cos7x-sin\frac{\pi}{3}\cdot sin7x=sin\frac{\pi}{6}\cdot sin5x+cos\frac{\pi}{6}\cdot cos5x[/m]

Применяем формулу ( см приложение)
[m]cos(3x+\frac{\pi}{3})=cos(x-\frac{\pi}{6})[/m]

[m]cos(3x+\frac{\pi}{3})-cos(x-\frac{\pi}{6})=0[/m]

Применяем формулу разности косинусов:

cos α –cos β


2.

Так же как преобразовали справа, только не делим на 2, а выносим 2 за скобки, а в квадрате это дает 4

Получим:

[m]4\cdot(sin\frac{\pi}{6}\cdot sinx+cos\frac{\pi}{6}\cdot cosx)^2-5=cos(\frac{\pi}{6}-x)[/m]

Замена
[m]cos(\frac{\pi}{6}-x)=cos(x-\frac{\pi}{6})=t[/m]

Квадратное уравнение

4t²–t–5=0

D=1–4·4·(–5)=81

t₁=–1; t₂=5/4

Обратная замена
[m]cos(x-\frac{\pi}{6})=-1[/m] ⇒ [m]x-\frac{\pi}{6}=2\pi n,[/m] n ∈ Z


[m]cos(x-\frac{\pi}{6})=\frac{5}{4}[/m] – не имеет корней

О т в е т. [m]x=\frac{\pi}{6}+2\pi n,[/m] n ∈ Z