Задача 33770 а) Решите уравнение 8sinx+4cos^2x = 7;...

vk295929291

2019-02-20 19:47:45

а) Решите уравнение 8sinx+4cos^2x = 7;

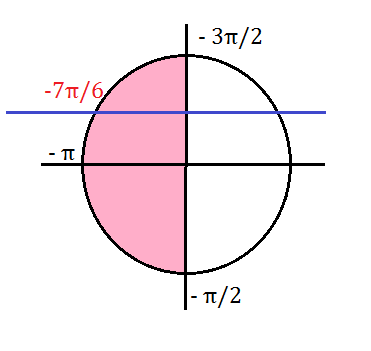
б) Найдите корни на отрезке [-3Pi/2; -Pi/2]

sova

2019-02-20 20:01:21

сos^2x=1-sin^2x
8sinx+4(1-sin^2x)=7
4sin^2x-8sinx +3=0

D=64-48=16

sinx=1/2 или sinx=3/2 ( не имеет корней, |sinx| ≤ 1)

x=(-1)^(k)arcsin(1/2)+πk, k ∈ Z

х=(-1))^(k)(π/6)+πk, k ∈ Z

х=-7π/6 ∈ [-3π/2;-π/2]