Задача 37098 ...
Условие
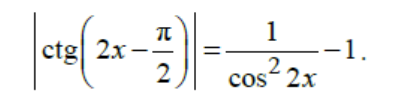
Решение
2x≠(π/2)+πr, r ∈ Z
[b] x≠(π/4)+(π/2)r, r ∈ Z[/b]
ctg(2x-(π/2))=-ctg((π/2)-2x)
ctg((π/2)-2x)=tg2x
(1/cos^22x) - 1= (1-cos^22x)/cos^22x=sin622x/cos^22x=tg^22x
|-tg2x|=tg^22x
Раскрываем знак модуля.
(1)
Если
-tg2x ≥ 0 ⇒ tg2x ≤ 0, то
|-tg2x|=-tg2x
уравнение принимает вид:
- tg2x=tg^22x
tg^22x+tg2x=0
tg2x*(tg2x+1)=0
tg2x=0 ⇒ 2x=πk, k ∈ Z ⇒ [b]x=(π/2)*k, k ∈ Z [/b]
или
tg2x+1=0 ⇒ tg2x=-1 ⇒ 2x=(-π/4)+πn, n ∈ Z ⇒ x=(-π/8)+(π/2)n, n ∈ Z
условию tg2x ≤ 0
удовлетворяют решения:
[b]х=(-π/8)+ πm, m ∈ Z[/b]
(2)
-tg2x ≤ 0 ⇒ tg2x ≥0, то
|-tg2x|=tg2x
уравнение принимает вид:
tg2x=tg^22x
tg^22x-tg2x=0
tg2x*(tg2x-1)=0
tg2x=0 ⇒ 2x=πk, k ∈ Z ⇒ [b]x=(π/2)*k, k ∈ Z [/b]
или
tg2x-1=0 ⇒ tg2x=1 ⇒ 2x=(π/4)+πn, n ∈ Z ⇒ x=(π/8)+(π/2)n, n ∈ Z
условию tg2x ≥ 0
удовлетворяют решения:
[b] x=(π/8)+ πm, m ∈ Z[/b]
Найденные корни удовлетворяют ОДЗ
О т в е т. (π/2)*k, k ∈ Z ; (-π/8)+ πm, m ∈ Z; (π/8)+ πm, m ∈ Z