Задача 64288 а)решите уравнение...

Витя_337310452

25 апреля 2022 г. в 16:53

а)решите уравнение 2cos(P/2–x)=tgx
б)[–2p;–p/2]

exponenta

25 апреля 2022 г. в 17:34

★

По формулам приведения

[m]cos (\frac{π}{2}-x)=sinx[/m]

Уравнение примет вид:

[m]2sinx=tgx[/m]

Так как [m]tgx=\frac{sinx}{cosx}[/m]

[m]2sinx=\frac{sinx}{cosx}[/m]

[m]2sinx-\frac{sinx}{cosx}=0[/m]

[m]sinx(2-\frac{1}{cosx})=0[/m]

[m]sinx=0[/m] ИЛИ [m]2-\frac{1}{cosx}=0[/m] ⇒ [m]cosx=\frac{1}{2}[/m]

[m]x=πk, k ∈ [/m] Z ИЛИ [m]x= ± \frac{π}{3}+2πn, n ∈ [/m] Z

О т в е т.

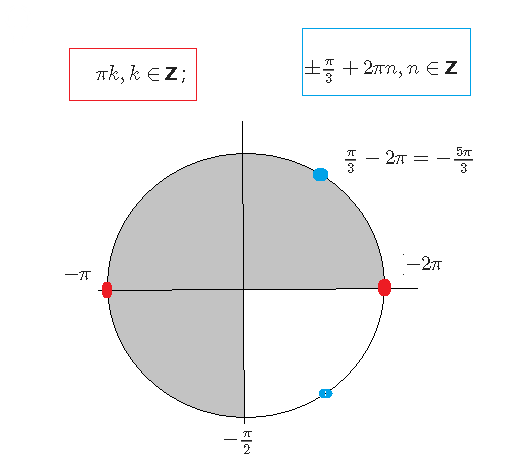
а) [m]πk, k ∈ [/m] Z ; [m] ± \frac{π}{3}+2πn, n ∈ [/m] Z

б)
Отрезку [m][-2π; -\frac{π}{2}][/m] принадлежат корни

[m] -2π; \frac{π}{3}-2π=-\frac{5π}{3}; -π[/m]

см. рис.