Задача 63385 ...

61d9de1eacffe413ad532e0b

26.02.2022 17:39:05

а) решите уравнение (1-3tg^(2)x)sqrt(7sinx)=0
б)найдите все корни этого уранения принадлежащие отрезку [-2π;-π/2]

5f3ea7e3faf909182968ddd9

26.02.2022 23:09:20

★

ОДЗ:
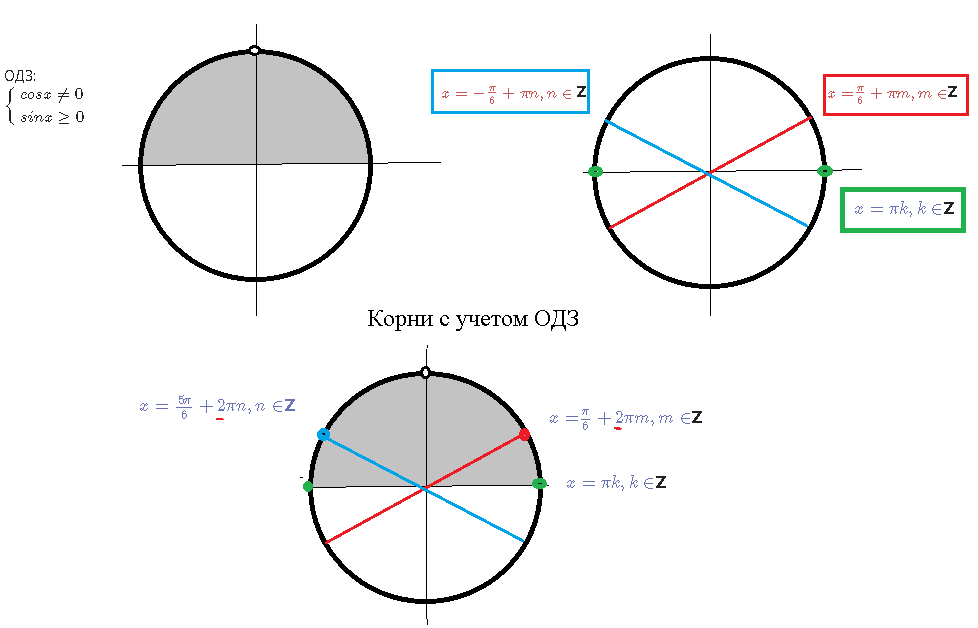
[m]\left\{\begin {matrix}cosx ≠ 0\\sinx ≥ 0\end {matrix}\right.[/m]


[m](1–3tg^2x)√7sinx=0[/m]

[m]1-3tg^2x=0[/m] ⇒[m] tg^2x=\frac{1}{3}[/m]

[m]tgx=-\frac{1}{\sqrt{3}}[/m] или [m]tgx=\frac{1}{\sqrt{3}}[/m]

[m]x=arctg(-\frac{1}{\sqrt{3}})+πn,n ∈[/m][b]Z [/b] или [m]x=arctg(\frac{1}{\sqrt{3}})+πm, m ∈[/m][b]Z [/b]

[red][m]x=-\frac{π}{6}+πn, n ∈[/m] [/red][b]Z [/b] или [red] [m]x=\frac{π}{6}+πm, m ∈[/m][/red][b]Z [/b]


[m]√7sinx=0[/m] ⇒ [m]sinx=0[/m] ⇒[red] [m]x=πk, k ∈ [/m][/red][b]Z [/b]


С учетом ОДЗ получаем ответ:

[blue][m]x=π-\frac{π}{6}+2πn, n ∈[/m][b]Z [/b] [/blue] или [blue] [m]x=\frac{π}{6}+2πm, m ∈[/m][/blue][b]Z [/b]

[blue][m]x=\frac{5π}{6}+2πn, n ∈[/m][b]Z [/b] [/blue]

[blue] [m]x=πk, k ∈ [/m][/blue][b]Z [/b]



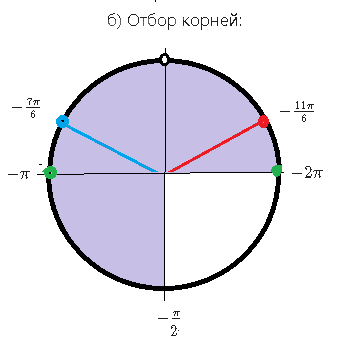
б) Отбор корней:

Отрезку
[–2π;–π/2] принадлежат корни:

[m]\frac{5π}{6}-2π=-\frac{7π}{6}[/m]


[m]\frac{π}{6}-2π=-\frac{11π}{6}[/m]


[m]-2π[/m] и [m]-π[/m]