Задача 31331 9. 7cos2x+18sin^2x-9 = 0 10....
Условие
10. cos2x+11sinx-6 = 0
11. 11sin2x+32sin^2x-12 = 0
12. 5cosx-10sinx-11 = 0
Решение
cos2x=1-2sin^2x
7*(1-2sin^2x)+18sin^2x-9=0;
4sin^2x-2=0
sin^2x=1/2
sinx= ± sqrt(2)/2
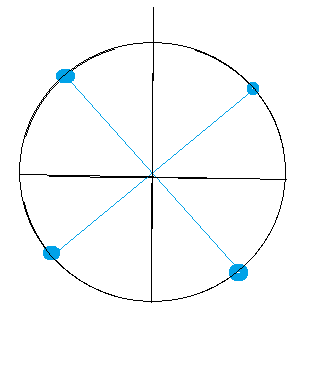
x= ± (π/4)+πm, m ∈ Z
См. рис. 1
10.
1-2sin^2x+11sinx-6=0
2sin^2x-11sinx+5=0
D=121-40=81
sinx=1/2 или sinx=5( не имеет корней, |sinx| ≤ 1)
x=(-1)^(k)*(π/6)+πk, k ∈ Z
О т в е т. (-1)^(k)*(π/6)+πk, k ∈ Z
11.
12=12*1=12*(sin^2x+cos^2x)
sin2x=2sinx*cosx
22sinx*cosx+32sin^2x-12sin^2x-12cos^2x=0
20sin^2x+22sinx*cosx-12cos^2x=0
10sin^2x+11sinx*cosx-6cos^2x=0
Делим на cos^2x ≠ 0
10tg^2x+11tgx-6=0
D=121-4*10*(-6)=121+240=361
tgx=(-11 ± 19)/20
tgx=-3/2 или tgx=0,4
x=arctg(-3/2)+πk, k ∈ Z или х=arctg0,4+πn, n ∈ Z
О т в е т. -arctg(3/2)+πk; arctg0,4+πn, k, n ∈ Z
12.
5cosx-10sinx=11
Применяем метод введения вспомогательного угла
5^2+10^2=25+100=125
Делим все члены уравнения на sqrt(125)
5/sqrt(125)cosx-(10/sqrt(125))sinx=11/sqrt(125)
cos φ cosx-sin φ sinx=11/sqrt(125)
cos(x+ φ )=11/sqrt(125)
x+ φ = ± arccos(11/sqrt(125))+2πn, n ∈ Z
x=± arccos(11/sqrt(125)) - φ +2πn, n ∈ Z
cos φ =5/sqrt(125)
sin φ =10/sqrt(125)
tg φ=2
О т в е т. ± arccos(11/sqrt(125)) - arccos(5/sqrt(125)) +2πn, n ∈ Z