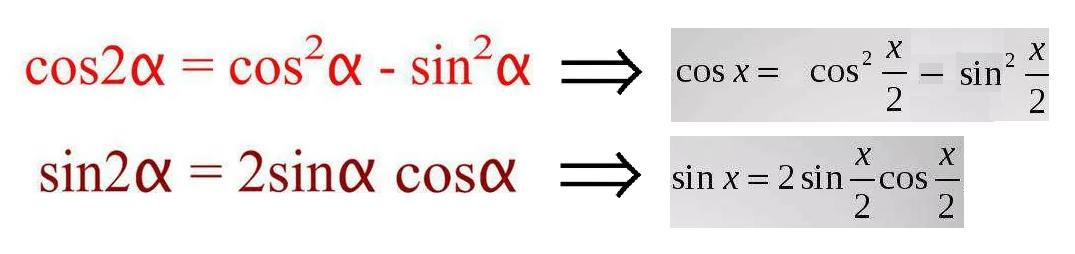Задача 59511 Решите уравнение 1+sinx+cosx =...
Условие
1+sinx+cosx = 2cos(x/2 - 45)
Решение
1+sinx=sin^2(x/2)+2sin(x/2)*cos(x/2)+cos^2(x/2)=([blue]sin(x/2)+cos(x/2)[/blue])^2
cosx=cos^2(x/2)-sin^2(x/2)=(cos(x/2)-sin(x/2))*([blue]cos(x/2)+sin(x/2)[/blue])
Уравнение принимает вид:
([blue]sin(x/2)+cos(x/2)[/blue])^2+(cos(x/2)-sin(x/2))*([blue]cos(x/2)+sin(x/2)[/blue])=sqrt(2)*[blue](cos(x/2)+sin(x/2))[/blue]
([blue]sin(x/2)+cos(x/2)[/blue])^2+(cos(x/2)-sin(x/2))*([blue]cos(x/2)+sin(x/2)[/blue])-sqrt(2)*[blue](cos(x/2)+sin(x/2))[/blue]=0
Раскладываем на множители:
[blue](cos(x/2)+sin(x/2))[/blue]*(cos(x/2)+sin(x/2)+cos(x/2)-sin(x/2)-sqrt(2))=0
[blue](cos(x/2)+sin(x/2))[/blue]*(cos(x/2)+cos(x/2)-sqrt(2))=0
1)
cos(x/2)+sin(x/2)=0
tg(x/2)=-1
(x/2)=(π/4)+πm, m ∈ Z
[b]x=(π/2)+2πm, m ∈ Z
[/b]
2)
cos(x/2)+cos(x/2)-sqrt(2)=0
cos(x/2)=sqrt(2)/2
x/2= ± (π/4)+2πk, k ∈ Z
[b]x=± (π/2)+4πk, k ∈ Z[/b]
О т в е т. (π/2)+2πm, m ∈ Z