Задача 33769 a) Решите уравнение...

vk295929291

2019-02-20 19:46:42

a) Решите уравнение [m]3\sqrt{3}cos\left(\frac{3\pi}{2} + x\right) - 3 = 2sin^{2}x[/m].

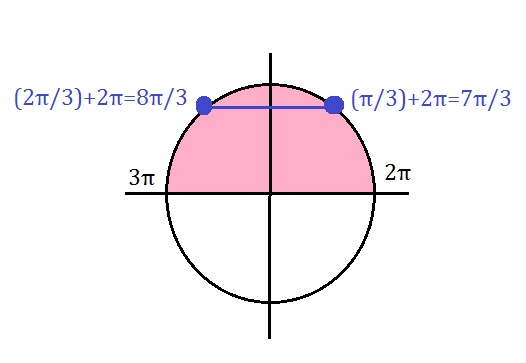
б) Укажите корни этого уравнения, принадлежащие отрезку [m][2\pi; 3\pi][/m].

sova

2019-02-20 20:11:57

cos((3π/2)+x)=sinx

3sqrt(3)sinx-3=2sin^2x

2sin^2x-3sqrt(3)sinx +3=0

D=27-4*2*3=3

sinx=(3sqrt(3)-sqrt(3))/4 или sinx=(3sqrt(3)+sqrt(3))/4;
sinx=sqrt(3)/2 или sinx=sqrt(3) не имеет корней

x=(-1)^(k)arcsin(sqrt(3))/2 +πk, k ∈ Z

х=(-1)^(k)(π/3) +πk, k ∈ Z - о т в е т.

х= (π/3) +2π=7π/3 ∈ [2π;3π]

х=(π-(π/3)+2π= 8π/3∈ [2π;3π]