Задача 63384 ...

61d9de1eacffe413ad532e0b

26.02.2022 17:36:22

а) решите уравнение sqrt(3)tgx+1/2sinx-1=0
б)найдите все корни этого уравнения принадлежащие этому отрезку [9π/2;6π]

5f3ea7e3faf909182968ddd9

26.02.2022 23:26:54

★

Дробь равна 0 когда числитель равен 0, а знаменатель отличен от нуля

[m]\left\{\begin {matrix}\sqrt{3}tgx+1=0\\2sinx-1 ≠ 0\end {matrix}\right.[/m]


[m]\left\{\begin {matrix}tgx=-\frac{1}{\sqrt{3}}\\sinx ≠ \frac{1}{2}\end {matrix}\right.[/m]


[m]\left\{\begin {matrix}x=arctg(-\frac{1}{\sqrt{3}})+πn, n ∈ Z\\x ≠(-1)^{k}arcsin \frac{1}{2}+πk, k ∈Z \end {matrix}\right.[/m]


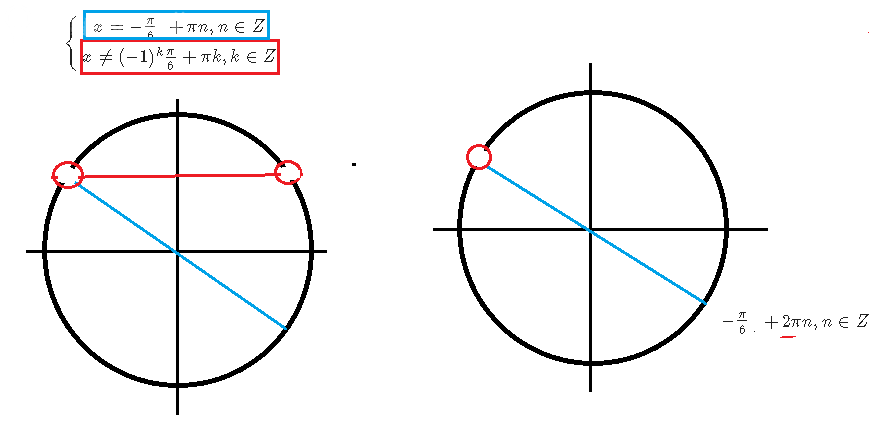
[m]\left\{\begin {matrix}x=-\frac{π}{6}+πn, n ∈ Z\\x ≠(-1)^{k}\frac{π}{6}+πk, k ∈Z \end {matrix}\right.[/m]

k=2m
[m]\left\{\begin {matrix}x=-\frac{π}{6}+πn, n ∈ Z\\x ≠\frac{π}{6}+2πm, m ∈Z \end {matrix}\right.[/m]

k=2m+1

[m]\left\{\begin {matrix}x=-\frac{π}{6}+πn, n ∈ Z\\x ≠-\frac{π}{6}+2π(m+1), m ∈Z \end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x=-\frac{π}{6}+πn, n ∈ Z\\x ≠\frac{5π}{6}+2πm, m ∈Z \end {matrix}\right.[/m] ⇒


О т в е т. [m]-\frac{π}{6}+2πn, n ∈ Z [/m]