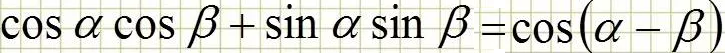Задача 43696 Решите тригонометрические уравнения...
Условие
Все решения
[m]\frac{1}{\sqrt{2}}cos3x+\frac{1}{\sqrt{2}}sin3x=1[/m]
Заменим
[m]\frac{1}{\sqrt{2}}=cos\frac{\pi}{4}[/m]
[m]\frac{1}{\sqrt{2}}=sin\frac{\pi}{4}[/m]
[m]cos\frac{\pi}{4}\cdot cos3x+sin\frac{\pi}{4}\cdot sin3x=1[/m]
[m]cos(3x-\frac{\pi}{4})=1[/m]
[m]3x-\frac{\pi}{4}=2\pi n[/m], n ∈ Z ⇒
[m]3x=\frac{\pi}{4}+2\pi n[/m], n ∈ Z ⇒
[m]x=\frac{\pi}{12}+\frac{2\pi}{3} n[/m], n ∈ Z - о т в е т
4.44
cos2x=cos^2x-sin^2x=(cosx-sinx)*(cosx+sinx)
1+sin2x=sin^2x+cos^2x+2sinx*cosx=(sinx+cosx)^2
(cosx-sinx)*(cosx+sinx)+(sinx+cosx)^2=0
(cosx+sinx)*(cosx-sinx+sinx+cosx)=0
cosx+sinx=0 или 2cosx=0
tgx=-1 или cosx =0
x=[b](-π/4)+πk, k ∈ Z[/b] или x=[b](π/2)+πn, n ∈ Z[/b]
