Задача 63317 а) решите уравнение...
Условие
б) найдите все корни этого уровнения, принадлежащие отрезку [7п/2;9п/2]
Решение
По формулам приведения:
[m]cos(\frac{π}{2}-x)=sinx[/m]
Уравнение можно записать в виде:
[m]4sin^3x=3\cdot sinx[/m]
[m]4sin^3x-3\cdot sinx=0[/m]
Раскладываем на множители:
[m]sinx\cdot (4sin^2x-3)=0[/m]
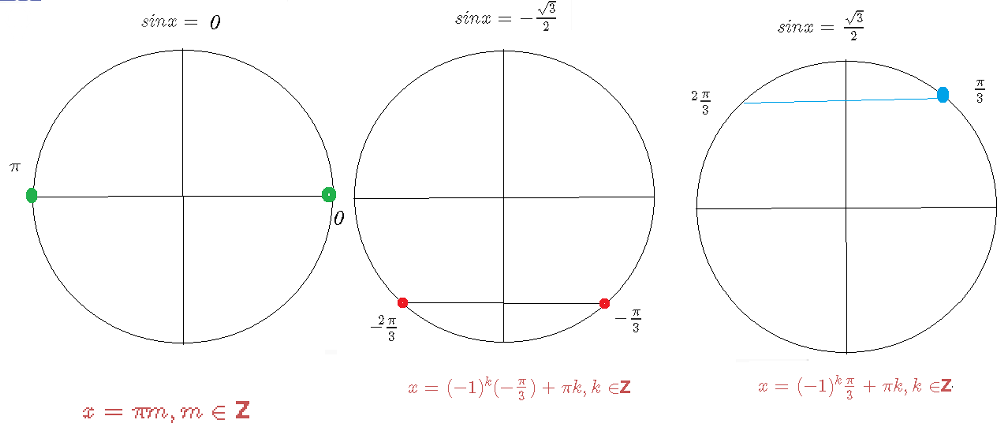
[m]sinx=0 [/m] или [m]4sin^2x-3=0[/m]
Решаем первое уравнение
[m]sinx=0 [/m] ⇒[red] [m]x=πm, m ∈ [/m] [b]Z[/b] [/red] - ответ первого уравнения
Решаем второе уравнение
[m]4sin^2x-3=0[/m] ⇒ [m]sin^2x=\frac{3}{4}[/m] ⇒ [m]sinx= ± \frac{\sqrt{3}}{2}[/m]
получили два простейших уравнения:
[m]sinx= - \frac{\sqrt{3}}{2}[/m] или [m]sinx= \frac{\sqrt{3}}{2}[/m]
Простейшее уравнение [m]sinx=a[/m] имеет смысл при -1 ≤ a ≤ 1
Решение находим по формуле: [red][m]x=(-1)^{k} arcsina+πk, k ∈ [/m][b]Z[/b][/red]
[m]sinx= - \frac{\sqrt{3}}{2}[/m]
[m]x=(-1)^{k} arcsin(- \frac{\sqrt{3}}{2})+πk, k ∈ [/m][b]Z[/b]
[red][m]x=(-1)^{k}(-\frac{π}{3})+πk, k ∈ [/m][b]Z[/b][/red] - ответ второго уравнения
[m]sinx= \frac{\sqrt{3}}{2}[/m]
[m]x=(-1)^{k} arcsin \frac{\sqrt{3}}{2}+πk, k ∈ [/m][b]Z[/b]
[red][m]x=(-1)^{k}\frac{π}{3}+πk, k ∈ [/m][b]Z[/b][/red]- ответ третьего уравнения
О т в е т.[m]πm, m ∈ [/m] [b]Z[/b] ;[m](-1)^{k}(-\frac{π}{3})+πk, k ∈ [/m][b]Z[/b];
[m](-1)^{k}\frac{π}{3}+πk, k ∈ [/m][b]Z[/b]
Б)
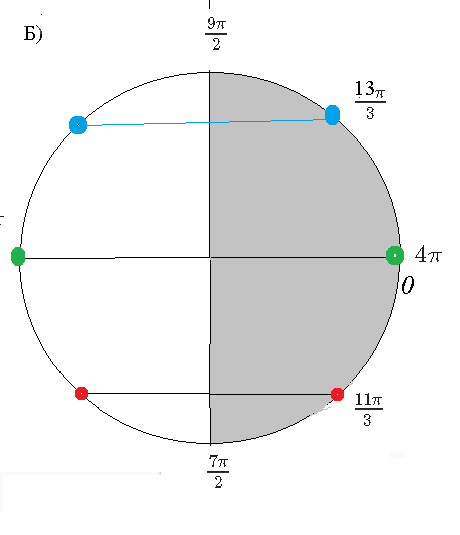
Отбираем корни.
Из первой серии ответов: [red] [m]x=πm, m ∈ [/m] [b]Z[/b] [/red]
Отрезку [[m]\frac{7π}{2};\frac{9π}{2}[/m]]
принадлежит корень [m]x=4\cdot π[/m]
[m]\frac{7π}{2}≤ 4π ≤ 1\frac{9π}{2}[/m]
Из второй серии ответов: [red][m]x=(-1)^{k}(-\frac{π}{3})+πk, k ∈ [/m][b]Z[/b][/red]
Отрезку [[m]\frac{7π}{2};\frac{9π}{2}[/m]]
принадлежит корень
[m]x=4π-\frac{π}{3}=\frac{11π}{3} [/m]
Из третьей серии ответов: [red][m]x=(-1)^{k}\frac{π}{3}+πk, k ∈ [/m][b]Z[/b][/red]
Отрезку [[m]\frac{7π}{2};\frac{9π}{2}[/m]]
принадлежит корень
[m]x=4π+\frac{π}{3}=\frac{13π}{3} [/m]
О т в е т. Отрезку [[m]\frac{7π}{2};\frac{9π}{2}[/m]]
принадлежат[b] три[/b] корня :
[m]4\cdot π[/m];
[m]\frac{11π}{3} [/m];
[m]\frac{13π}{3} [/m]